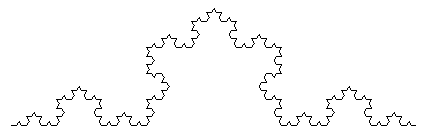
Рисуем кривую Коха и снежинку Коха

Прежде чем идти дальше, давайте познакомимся с turtle-графикой (то есть, черепашьей графикой) в Python. С ее помощью часто выполняется рисование фракталов с помощью, так называемых, L-систем, о которых мы еще будем говорить. А пока посмотрим, как эта «черепашка» сможет нарисовать нам первые фракталы – кривую и снежинку Коха.

Принцип здесь очень простой. Черепашка может ползти вперед (то есть, куда глаза глядят) с помощью команды forward(), поворачиваться влево, вправо с помощью команд left() и right(). И делать некоторые другие элементы «высшего пилотажа», с которыми мы постепенно познакомимся. Если вы хотите сразу поближе познакомиться с черепашкой, то это можно сделать по ссылке:

https://docs.python.org/3/library/turtle.html

Итак, чтобы запустить черепашку в нашу программу, достаточно сделать импорт:

import turtle

а, затем, создать ее экземпляр:

t = turtle.Turtle()

Если сейчас запустить программу, то появится графическое окно и тут же пропадет. Чтобы этого не происходило, в конце добавим команду:

turtle.done()

Отлично, наша черепашка готова беспрекословно выполнять любые команды. Скажем ей пройти вперед на 20 пикселей:

t.forward(20)

или в сокращенном варианте:

t.fd(20)

Далее, повелим ей повернуться налево на 90 градусов, пройти еще 20 писелей, повернуться направо на 120 градусов и пройти еще 40 пикселей:

t.left(90)
t.fd(20)
t.right(120)
t.fd(40)

Как видите, она послушно выполнила все наши команды. Пришло время дать нашей черепашке настоящее задание. Объявим функцию, которая нарисует один сегмент кривой Коха:

def draw_koch_segment(t, ln):
    t.fd(ln)
    t.left(60)
    t.fd(ln)
    t.right(120)
    t.fd(ln)
    t.left(60)
    t.fd(ln)

Чтобы рисование происходило быстрее, мы ускорим черепашку командой:

t.speed(100)

Итак, одна итерация у нас есть. Теперь, каждый линейный фрагмент также нужно прорисовать такой же ломаной, но уменьшенной в 3 раза. Проще всего это сделать через рекурсию, следующим образом:

def draw_koch_segment(t, ln):
    if ln > 6:
        ln3 = ln // 3
        draw_koch_segment(t, ln3)
        t.left(60)
        draw_koch_segment(t, ln3)
        t.right(120)
        draw_koch_segment(t, ln3)
        t.left(60)
        draw_koch_segment(t, ln3)
    else:
        t.fd(ln)
        t.left(60)
        t.fd(ln)
        t.right(120)
        t.fd(ln)
        t.left(60)
        t.fd(ln)

Мы заменяем линейные сегменты, пока длина сегмента ln больше 6 пикселей. Соответственно, при выполнении этого условия, уходим вглубь рекурсии и черепашка готова прорисовывать более мелкие детали. Когда условие не выполняется, то начинается рисование, причем, только самых мелких деталей. Фактически, рекурсией мы здесь сформировали множество однотипных команд для проприсовки кривой Коха.

Давайте запустим эту функцию, прописав такие строчки:

ln = 150
t.ht()
draw_koch_segment(t, ln)

Здесь ln = 150 – это длина одного линейного сегмента на самом крупном масштабе; команда th() скрывает черепашку. После выполнения увидим следующее изображение:

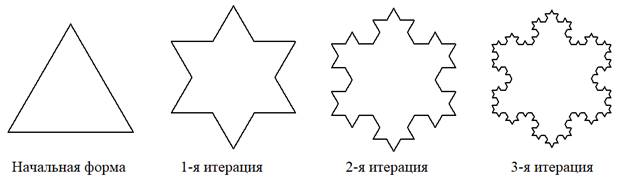
Черепашка успешно справилась со своей миссией и нарисовала нам первый фрактал.

Следующим шагом нарисуем снежинку Коха. Как мы отмечали на прошлом занятии, основой для нее служит равносторонний треугольник, в котором линейные сегменты постепенно заменяются все той же ломаной:

Как это сделать нам в нашей программе? Нет ничего проще. Функция draw_koch_segment() рисует один линейный сегмент начального треугольника. Значит, для прорисовки всех трех сторон, мы будем поворачивать черепашку вправо на 120 градусов и снова выполнять эту же функцию:

draw_koch_segment(t, ln)
t.right(120)
draw_koch_segment(t, ln)
t.right(120)
draw_koch_segment(t, ln)

В результате получим это:

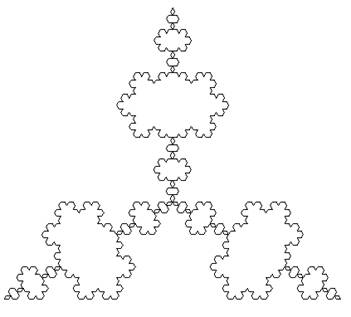
Кстати, если вместо поворота вправо на 120 градусов сделать поворот влево, то получим уже друое изображение:

draw_koch_segment(t, ln)
t.left(120)
draw_koch_segment(t, ln)
t.left(120)
draw_koch_segment(t, ln)

Тоже весьма достойная картина. Вот на что способна наша черепашка. И это только начало. На следующем занятии мы познакомимся с универсальным способом формирования множества разных фракталов, известный как L-система.

Рисуем кривую Коха и снежинку Коха

Видео по теме