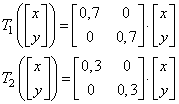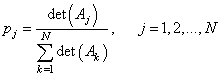|
Рандомизированная система итерированных функцийАрхив проекта: 11_fractals.py На прошлом занятии мы с вами реализовали простую систему итерированных функций для формирования фрактала «ковер Серпинского». Для этого было использовано три сжимающих отображения для формирования множества точек на текущей итерации:
Так вот, это
множество точек оказывается неизменным, вне зависимости от конфигурации
начального компактного множества
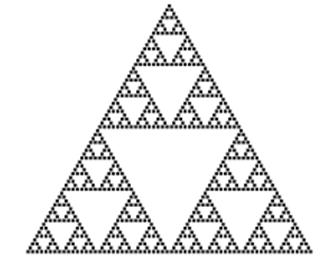
В пределе, при числе итераций, стремящихся к бесконечности, мы все равно получим фрактал «ковер Серпинского» при заданных сжимающих отображениях:
И это важный
момент. Фактически, это означает, что СИФ набором сжимающих функций Давайте для
примера возьмем произвольную точку, допустим с координатами
Получим новую
точку
И так далее. Через n итераций у нас будет n+1 точка:
Так вот, где бы
мы не взяли начальную точку
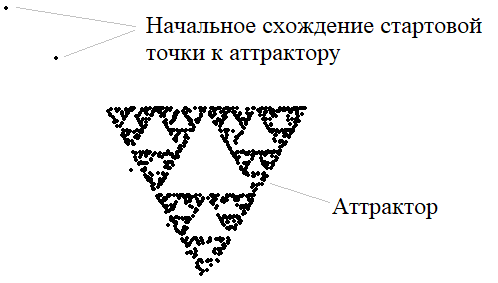
Реализуем этот простой алгоритм на Python. Для этого мы в класс SIF, который сформировали на прошлом занятии, добавим метод для получения следующей точки: def get_next_point(self, pos, pt, scale): indx = random.randint(0, len(self.T)-1) pt_new = self.T[indx][0] @ pt + self.T[indx][1] * scale + pos return (pt_new[0], pt_new[1]) Здесь на вход мы подаем координату pos точки смещения рисования точек; текущую точку pt; и масштаб фигуры scale. Затем, случайным образом выбираем одно из сжимающих отображений и применяем его к текущей точке pt. На выходе формируем точку с новыми координатами. Чтобы в нашем классе SIF было свойство self.T, в конструкторе класса пропишем: class SIF: def __init__(self, coeffs): self.coeffs = coeffs self.T = self.create_funcs() И соответствующую строчку уберем из метода create_attractor(). Далее, создадим экземпляр класса и определим следующие вспомогательные переменные: sif = SIF(C) pt = (0, 0) scale = (200, 200) pos = (100, 100) А главный цикл запишем в виде: n_iter = 1 while True: for event in pygame.event.get(): if event.type == pygame.QUIT: exit() if n_iter < 1000: pygame.draw.circle(sc, BLACK, (round(pt[0]), round(pt[1])), 2) pt = sif.get_next_point( pos, pt, scale ) n_iter += 1 pygame.display.update() clock.tick(FPS) То есть, на каждой итерации мы рисуем точки на плоскости sc в виде черных кружочков радиусом в 2 пиксела. После запуска программы увидим следующее изображение:
То есть, здесь начальная точка с координатами (0; 0) сначала последовательно приближалась к аттрактору динамической системы, а затем, оказавшись в нем, уже практически не выходит за его пределы. Получается, что набор сжимающих отображений действительно описывают некоторое замкнутое множество точек, которые описывают, в данном случае фрактал «ковер Серпинского». Кроме того, мы с вами получили еще один алгоритм формирования фракталов с помощью СИФ, известный в литературе как рандомизированная СИФ. Но в реализованном нами алгоритме есть один существенный недостаток: равная вероятность применения того или иного сжимающего отображения. Казалось бы, это вполне логично – каждое преобразование нужно брать с равной вероятностью. Или, все же нет? Давайте представим, что есть два преобразования, но с разной степенью сжатия:
Тогда размеры
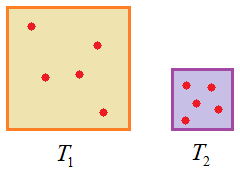
множеств, которые они описывают, будут разными. И если выбирать их с равной
вероятностью, то плотность точек для первого преобразования будет заметно ниже,
чем для второго. Визуально это может сильно бросаться в глаза. Очевидно, здесь
отображение Нам опять на помощь приходит математика. Если вспомнить, что геометрический смысл определителя матрицы (2х2) – это площадь параллелограмма, образованная его векторами:
То мы можем воспользоваться этой мерой для определения вероятностей выбора сжимающих отображений:
Давайте реализуем эту логику в нашей рандомизированной СИФ. Для этого я задам еще один метод get_probabilities() в классе SIF, который и будет вычислять эти вероятности: def get_probabilities(self): dets = [np.abs(np.linalg.det(t[0])) + 0.1 for t in self.T] s = sum(dets) return [d/s for d in dets] Определитель вычисляется с помощью функции det() ветки numpy.linalg, затем, все значения суммируются и вычисляются вероятности. Далее, нам нужно выбирать отображения в соответствии с этими вероятностями. Мы это с вами уже делали, когда рассматривали стохастическую L-систему, поэтому, я просто приведу метод, который будет выбирать случайным образом сжимающее отображение: def get_random_T(self, pr): p = random.random() # случайное вещественное число в интервале [0; 1] off = 0 for i, pt in enumerate(pr): if p < (pt+off): return self.T[i] off += pt return False А сам метод get_next_point() следует скорректировать, следующим образом: def get_next_point(self, pos, pt, scale): p = self.get_probabilities() t = self.get_random_T(p) if not t: return pt pt_new = t[0] @ pt + t[1] * scale + pos return (pt_new[0], pt_new[1]) Все, у нас получилась полноценная рандомизированная СИФ и при запуске мы увидим тот же аттрактор в виде ковра Серпинского. Видео по теме |
:
описывает
конфигурации некоторого неизменного множества точек (в данном случае на
плоскости). И это множество точек есть не что иное как аттрактор (то
есть, предельный маршрут движения, изменения) заданной динамической системы. Аттрактор
еще можно воспринимать как кривую сгущения, к которой стремятся точки
динамической системы. И мы можем в этом легко убедиться.
и
применим к ней одно из сжимающих преобразований, выбранное случанйм образом:
с
другими координатами. Затем, к ней также применим случано выбранное
отображение для получения третьей точки:
(с
любыми координатами), множество точек будет последовательно приближаться к
аттрактору, определяемый сжимающими отображениями:
нужно
выбирать чаще, чем 
.
Но как это сделать?
