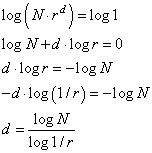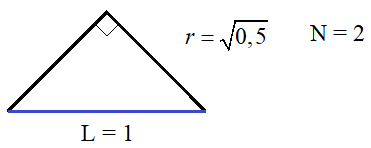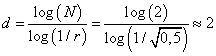|
Как вычисляется фрактальная размерность по ХаусдорфуНа предыдущих занятиях мы с вами последовательно рассматривали разные вариации L-системы по принципу «от простого к сложному». Я решил не прерывать это повествование и довести его до логического конца. Теперь же можно вернуться к одному важному вопросу, который остался в стороне – о вычислении размерности фрактальных кривых. Как я говорил во введении, фракталы принадлежат дробной размерности. Например, кривая Коха имеет размерность, равную, примерно, 1,2618. Но как она была вычислена? Именно это мы и разберем на этом занятии.
Первый математический аппарат для расчета дробных размерностей предложил немецкий ученый Феликс Хаусдорф в 1919 году.
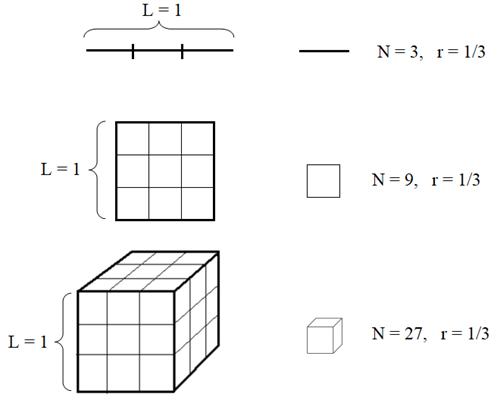
Феликс Хаусдорф (1868-1942 гг.) Чтобы получить формулу расчета размерности фигуры, можно рассуждать следующим образом. Если взять линейный отрезок и разделить его на N = 3 равные части, то длина каждого фрагмента будет в три раза меньше исходной длины. Пусть начальная длина, условно равна 1, тогда длины фрагментов будут равны r = 1/3. Очевидно, что общая длина отрезка, равна:
Проделаем ту же операцию с квадратом. Каждую из его сторон длиной в одну единицу также разделим на три равные части. То есть, линейные размеры маленьких квадратов будут равны r = 1/3. И таких квадратов всего N = 9. В этом случае площадь большого квадрата будет равна:
Как вы уже догадались, если взять куб и каждую из его сторон также разбить на три равных отрезка, то получим N = 27 кубиков со сторонами r = 1/3. Тогда объем куба можно выразить формулой:
То есть, смотрите, размерность фигуры проявляется как степень коэффициента подобия r. И в общем случае можно записать:
Чтобы из этой формулы выразить степень d, прологарифмируем левую и правую части этого уравнения, получим:
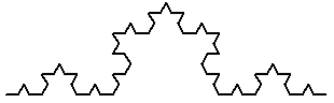
Логарифм можно взять по любому основанию, обычно это 2, 10 или e – натуральный логарифм. Величину d называют фрактальной размерностью или размерностью подобия. Вот это выражение и есть формула Хаусдорфа для вычисления размерностей произвольных кривых, которые могут быть разбиты на одинаковые фрагменты. Фрактальные кривые, как раз обладают таким свойством – они составлены их однотипных кривых меньшей размерности поэтому принцип расчета размерности, предложенный Хаусдорфом, хорошо для них подходит. Давайте воспользуемся этой формулой, вычислим размерность кривой Коха и проверим, действительно ли она равна 1,2816.
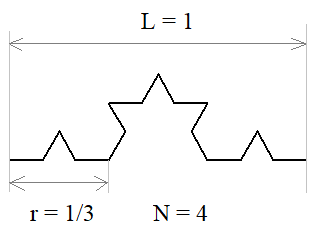
Смотрите, длина уменьшенных сегментов равна r = 1/3 от общей длины L = 1. Всего таких сегментов N = 4. Подставляем величины в формулу фрактальной размерности, имеем:
Давайте проделаем тот же ход для вычисления размерности фрактала «ковер Серпинского».
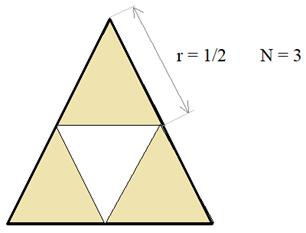
Здесь коэффициент подобия r = 1/2. Всего уменьшенных треугольников N = 3. Получаем размерность этого фрактала, равной:
Ну и последний пример – размерность фрактала «дракон Хартера-Хейтуэя».
На каждой
итерации прямые заменяются на прямоугольные уголки. Если длину прямой принять
за единицу (L = 1), то длины
сторон прямоугольного уголка будут равны
То есть, при числе итераций стремящихся к бесконечности, дракон покроет собой все двумерное пространство. На самом деле – это один из примеров кривой Пеано, которая будучи одномерной, способна обходить все точки на плоскости. И метрика Хаусдорфа это подтверждает. Видео по теме |