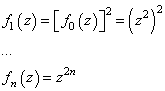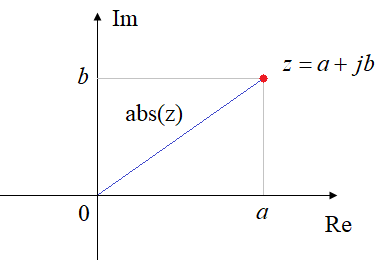|
Как построить множества ЖюлиаАрхив проекта: 13_fractals.py На прошлых занятиях мы с вами рассмотрели способы построения фракталов с помощью L-систем, предложенные венгерским биологом Аристидом Линденмайером в 1968 году, с помощью систем итерированных функций, разработанные Джоном Хатчинсоном и Майклом Барнсли в 1981 году. Но есть еще один довольно известный метод построения фракталов, с которого, фактически, и начался подъем этого научного направления – формирование фрактальных кривых как аттракторов динамических систем. В период с 1917
по 1919 годы французский математик Гастон Жюлиа (1893-1978 гг.) одновременно с
Пьером Фату (1878-1929 гг.) исследовали итерирование функций комплексного
переменного. Они изучали поведение полиномов степени
где
И смотреть, как она себя будет вести на итерациях:
Это напоминает СИФ с одним сжимающим отображением. Но даже в таком простом варианте можно получать удивительные по красоте изображения. И мы с вами скоро в этом убедимся.
Итак, как же эта функция комплексного переменного способна генерировать фрактальные кривые? В данном случае, мы можем получить только два аттактора: первый в виде множества точек на единичной окружности; второй – точка ноль. Почему именно такие аттракторы? Если кто из вас не знает, то любое комплексное число вида:
где a –
действительная часть числа; b – мнимая часть;
Из этого рисунка хорошо видно, что точки, которые при большом числе итераций не уходят в бесконечность:
это те, для которых модуль комплексного числа z меньше или равен единице:
Например, если число по модулю равно 0,7, то постоянно возводя его в квадрат, будем получать все меньшие и меньшие значения, пока в пределе не дойдем до нуля. А единица в любой степени всегда единица:
Поэтому, здесь мы и получаем, что любая комплексная точка, лежащая на единичной окружности, на ней и остается при любом числе итераций функции комплексного переменного. И то же самое с нулем. То есть, аттрактор состоит из множества «устойчивых» точек, не меняющих свое положение при итерировании функции. Множество точек на комплексной плоскости, которые не уходят в бесконечность при увеличении числа итераций n, образуют множества Жюлиа. Однако, рисовать круги путем многократного повторения функции комплексной переменной – это не лучшее занятие. На что еще способны эти формулы? Давайте сделаем простую вещь – добавим комплексное слагаемое и рассмотрим функцию вида:
Казалось бы, что это слагаемое может поменять? Но оно буквально разрывает круг и приводит к многочисленным причудливым фрактальным формам! Прежде чем посмотреть на очередное чудо, нужно выяснить, при каких значениях
функция при итерациях не будет уходить в бесконечность. Вы думаете это то же значение 1, как и в предыдущем случае? Нет, тут следует уже брать значение 2. Почему? Есть теорема, которая доказывает, что любое комплексное число в такой функции при
заведомо будет уходить в бесконечность. А, значит, она не принадлежит множеству Жюлиа. (Формулировку и доказательство этой теоремы можно найти практическим в любом учебнике по фрактальным процессам).
Например, вот так выглядят множества Жюлиа при разных значениях слагаемого c. Точки, которые закрашены черным цветом – это точки множества, а остальные – это точки вне множества. Настало время и нам создать сие творение собственноручно. Идея алгоритмов, которые строят такие множества, следующая.
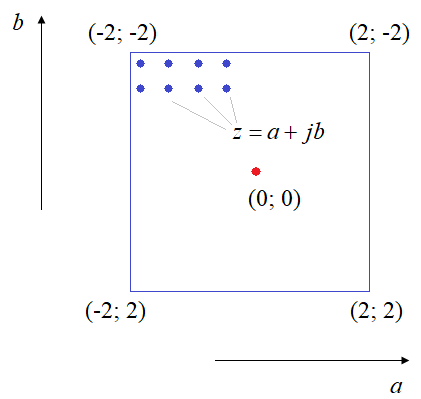
Мы сканируем множество точек на комплексной плоскости, например, в диапазоне [-2; 2] по мнимой и действительной осям. Каждая точка – это комплексное число:
Наша задача определить, относится ли эта точка к множеству Жюлиа или нет. Для этого, мы делаем n итераций для функции:
где c – заданное комплексное число (константа). Если окажется, что после n итераций модуль полученного комплексного числа меньше двух, то такую точку следует отнести к множеству Жюлиа:
Иначе, это точка фона. Строим множества Жюлиа на PythonДавайте реализуем такой алгоритм на Python с использованием Pygame. Вначале мы инициализируем Pygame, следующим образом: import pygame import os WHITE = (255, 255, 255) BLACK = (0, 0, 0) # ---------- чтобы окно появлялось в верхнем левом углу ------------ x = 20 y = 40 os.environ['SDL_VIDEO_WINDOW_POS'] = "%d,%d" % (x,y) # -------------------------------------------------------------------- pygame.init() W = 1200 H = 600 sc = pygame.display.set_mode((W, H)) pygame.display.set_caption("Множества Жюлиа") sc.fill(WHITE) FPS = 30 # число кадров в секунду clock = pygame.time.Clock() while True: for event in pygame.event.get(): if event.type == pygame.QUIT: exit() pygame.display.update() clock.tick(FPS) Здесь вам должно быть все понятно, мы делали это несколько раз на прошлых занятиях. Далее, в программе (до главного цикла) определим комплексную константу, размер формируемого изображения, масштабный коэффициент и число итераций для проверки принадлежности точки к множеству Жюлиа: c = complex(-0.2, 0.75) P = 200 # размер [2*P+1 x 2*P+1] scale = P / 2 # масштабный коэффициент n_iter = 100 # число итераций для проверки принадлежности к множеству Жюлиа После этого выполним цикл по множеству точек и те их их, что принадлежат множеству Жюлиа, закрасим в черный цвет: for y in range(-P, P): for x in range(-P, P): a = x / scale b = y / scale z = complex(a, b) for n in range(n_iter): z = z**2 + c if abs(z) > 2: break else: pygame.draw.circle(sc, BLACK, (x + P, y + P), 0) Смотрите, когда мы делим текущие координаты (x, y) на масштаб scale, то все значения комплексного числа z у нас пробегают диапазон [-2; 2] по каждой из осей. То есть, мы точки изображения отображаем в комплексную плоскость в квадрат диапазона [-2; 2]. Далее, делаем 100 итераций и если цикл завершается штатно, то есть, модуль точки не превысил порогового значения 2, то делаем вывод, что это точка множества Жюлиа и мы ее закрашиваем черным цветом. После запуска программы увидим следующее изображение:
Это множество
точек для константы
Таким образом, меняя константы c можно получать самые разные конфигурации множества Жюлиа. И это только один вид функции:
В общем случае
можно брать произвольные функции полиномов степени
и получать более сложные виды конфигураций множеств. Но мы остановимся на этом виде функции и следующим шагом выполним раскраску этого множества для лучшего визуального восприятия. Для этого в цикле формирования точек, внесем следующие изменения: for y in range(-P, P): for x in range(-P, P): a = x / scale b = y / scale z = complex(a, b) n = 0 for n in range(n_iter): z = z**2 + c if abs(z) > 2: break if n == n_iter-1: r = g = b = 0 else: r = (n % 2) * 32 + 128 g = (n % 4) * 64 b = (n % 2) * 16 + 128 pygame.draw.circle(sc, (r, g, b), (x + P, y + P), 0) Мы здесь после цикла итераций проверяем, если дошли до конца цикла, значит, точка относится к множеству и по прежнему отображаем ее черным цветом. Иначе, для других точек, не входящих в множество, формируем цвета в зависимости от удаленности точки от границы множества, то есть, в зависимости от значения n. Здесь приведены выражения, которые я подобрал путем «тыка», чтобы получались привлекательные цвета. В итоге, имеем следующее:
Здорово, правда? Можно подобрать и другие константы. Я приведу небольшой их список на языке Python: #c = complex(-1) #c = complex(-0.2, 0.75) #c = complex(-0.1244, 0.756) #c = complex(-0.1194, 0.6289) #c = complex(-0.7382, 0.0827) c = complex(0.377, -0.248) Попробуйте и посмотрите, что у вас получится. Мало того, мы легко можем менять масштаб изображения. Если переменную scale установить равной: scale = P / 1 то изображение станет больше (как бы ближе к наблюдателю):
Это из-за того, что мы пробегаем квадрат [-1; 1] на комплексной плоскости с той же плотностью точек. В результате, как бы рассматриваем это изображение с большей детализацией. Если нам нужно приблизить масштаб относительно произвольной точки, то для этого достаточно задать переменную с координатами смещения: scale = P / 0.25 # масштабный коэффициент view = (0, -500) # координаты смещения угла обзора В циклах учесть это смещение: for y in range(-P+view[1], P+view[1]): for x in range(-P+view[0], P+view[0]): И при отображении точки: pygame.draw.circle(sc, (r, g, b), (x + P - view[0], y + P - view[1]), 0) Все, теперь, мы можем увеличить и детальнее рассмотреть верхний участок этого множества:
Вот такие изображения можно получать с помощью одной единственной функции с проверкой ее сходимости в различных точках комплексной плоскости. Надеюсь, из этого занятия вы теперь лучше стали понимать что такое множество Жюлиа, как его можно построить и раскрасить. На следующем занятии мы проделаем похожие манипуляции для построения самого известного фрактального множества Мандельброта. Видео по теме |
вида:
-
комплексные числа. Например, в самом простом случае, можно взять функцию вида:
,
-
мнимая единица. Можно представить как точку на комплексной плоскости:
.
Если взять другую константу 
, то
получим другое множество точек:
