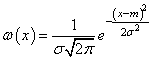|
Добавляем случайности в L-системуАрхив проекта: 7_fractals.py На прошлом занятии мы с вами добавили параметры в L-систему. Но этого недостаточно, чтобы генерировать близкие к природным фрактальные изображения и процессы. Не хватает, возможно, самого главного – случайностей при развитии фрактальных кривых. Без этого изображения на выходе L-систем будут выглядеть одинаково и однотипно, что не согласуется с визуальным восприятием реальных природных объектов, в которых практически всегда присутствуют элементы случайного изменения. На этом занятии мы добавим такой элемент в нашу L-систему и сделаем ее стохастической, то есть, со случайным поведением. Что понимается под случайностью L-системы? Как правило, два момента:
Начнем с самого простого – добавим случайности в параметры L-системы. Например, для поворотов налево и направо у нас имеются соответствующие функции. Что если прямо в них прописать случайное изменение параметра угла поворота, следующим образом: def cmd_turtle_left(t, angle, *args): d = random.random()*20 - 10 t.left(angle * args[0] + d) Здесь функция random() модуля random возвращает случайное число в интервале [0; 1], мы его умножаем на 20 и вычитаем 10, получаем интервал вещественных чисел в диапазоне [-10; 10]. Однако, еще немецкий математик Даниил Бернули заметил, что: Если данные из повседневной жизни не подчиняются нормальному закону, то значит в них что-то не так. Другими словами, случайные отклонения параметров в природных являениях, обычно, подчиняются нормальному закону:
где m и σ – математическое ожидание (среднее значение) и дисперсия (мера разброса) СВ X:
Однако, в
«чистом» виде СВ, подчиняющаяся нормальному закону распределения имеет интервал
random.gauss(mu, sigma) А ограничение максимальных отклонений с помощью функции: random.triangular(-off, off, random.gauss(mu, sigma)) То есть, в нашем случае случайность поворота можно определить так: def cmd_turtle_left(t, angle, *args): off = 20 # границы интервала [-20; 20] mu = 0 # среднее значение СВ (матю ожижание) sigma = 10 # дисперсия (мера разброса) СВ d = random.triangular(-off, off, random.gauss(mu, sigma)) t.left(angle * args[0] + d) Если запустить программу, то мы увидим эти случайные отклонения при поворотах налево. Но такая реализация случайностей в параметрах – не лучший ход. Так как на следующей итерации построения кривой снова будет использоваться прежний угол в angle градусов. То есть, добавленная случайность угла присутствует исключительно на текущей ветке.
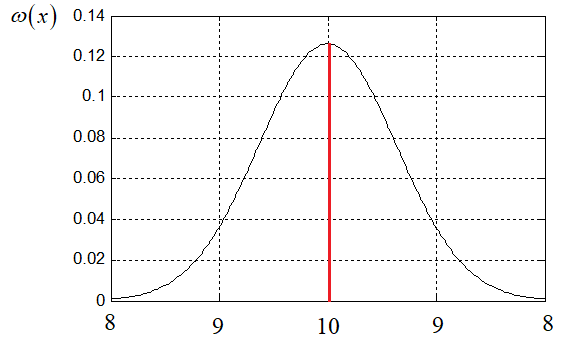
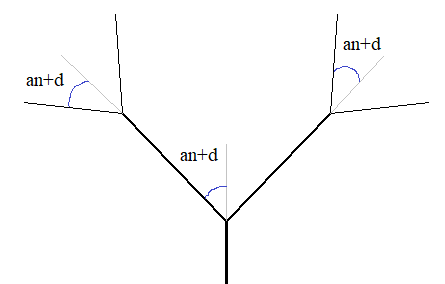
Если мы хотим именно этого, то такая реализация оправдана. Но если нам нужно, чтобы измененный угол на случайную величину d на предыдущей итерации учитывался на следующей, то случайное изменение нужно выполнять на уровне правил:
Поэтому, я оставлю в функциях cmd_turtle_left и cmd_turtle_right только угол: def cmd_turtle_left(t, angle, *args): t.left(args[0]) def cmd_turtle_right(t, angle, *args): t.right(args[0]) А в правилах пропишу его непосредственно в параметре: l_sys.add_rules(("A", f"F(1, 1)[+({angle})A][-({angle})A]"), ("F(x, y)", lambda x, y: f"F({1.5*x}, {1.7*y})"), ("+(x)", lambda x: f"+({x + random.triangular(-10, 10, random.gauss(0, 2))})"), ("-(x)", lambda x: f"-({x + random.triangular(-10, 10, random.gauss(0, 2))})"), ) Точно также мы можем менять и длину ветвей: l_sys.add_rules(("A", f"F(1, 1)[+({angle})A][-({angle})A]"), ("F(x, y)", lambda x, y: f"F({(1.2+random.triangular(-0.5, 0.5, random.gauss(0, 1)))*x}, {1.4*y})"), ("+(x)", lambda x: f"+({x + random.triangular(-10, 10, random.gauss(0, 2))})"), ("-(x)", lambda x: f"-({x + random.triangular(-10, 10, random.gauss(0, 2))})"), ) Теперь дерево выглядит более разнообразно. Фактически, вот так достаточно просто мы с вами прописали случайности в L-системе на уровне параметров. При этом даже не пришлось переписывать класс LSystem2D. Случайный выбор правил L-системыСледующим шагом сделаем возможность случайного выбора правила при формировании фрактальной кривой. Обычно, для этого определенной команде ставится в соответствие несколько правил:
Здесь
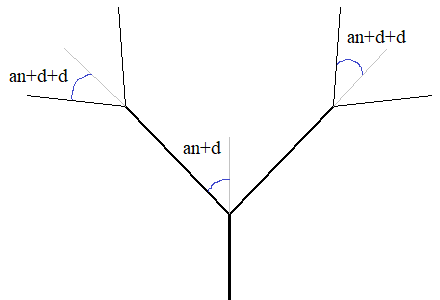
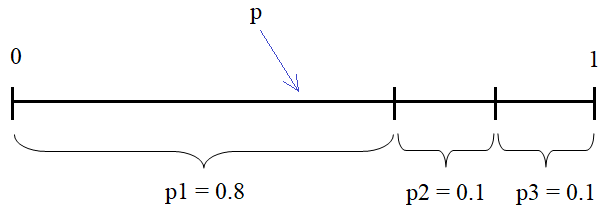
так как одно из правил на каждой итерации все же нужно выбрать. Такого функционала в нашей L-системе еще нет, поэтому добавим его. Для начала положим, что одной и той же команде (символу) можно ставить в соответствие несколько правил, причем третьим параметром будем указывать вероятность его выбора на каждой итерации: l_sys.add_rules(("A", f"F(1, 1)[+({angle})A][-({angle})A]", 0.9), ("A", f"F(1, 1)[+({angle})O][-({angle})A]", 0.05), ("A", f"F(1, 1)[+({angle})A][-({angle})O]", 0.05), ("F(x, y)", lambda x, y: f"F({(1.2+random.triangular(-0.5, 0.5, random.gauss(0, 1)))*x}, {1.4*y})"), ("+(x)", lambda x: f"+({x + random.triangular(-10, 10, random.gauss(0, 2))})"), ("-(x)", lambda x: f"-({x + random.triangular(-10, 10, random.gauss(0, 2))})"), ) Если в кортеже только два элемента, то вероятность выбора правила автоматически будет равна единице, то есть, срабатывать всегда. Далее, нам нужно изменить метод add_rules(), чтобы можно было назначать несколько правил одному ключу. В цикле будем перебирать переданный список кортежей и если в нем три элемента, то формируем значения переменных key, value, p, иначе (при двух элементах), формируются только два значения key, value: def add_rules(self, *rules): for r in rules: p = 1 # вероятность выполнения правила, если она не указана if len(r) == 3: key, value, p = r else: key, value = r key_re = key.replace("(", r"\(") key_re = key_re.replace(")", r"\)") key_re = key_re.replace("+", r"\+") key_re = key_re.replace("-", r"\-") if not isinstance(value, str): # ключ с параметрами key_re = re.sub(r"([a-z]+)([, ]*)", lambda m: r"([-+]?\b\d+(?:\.\d+)?\b)" + m.group(2), key_re) self.key_re_list.append(key_re) if not self.rules.get(key): self.rules[key] = [(value, key_re, p)] else: self.rules[key].append((value, key_re, p)) Затем, мы для каждого символа-ключа определим переменную key_re. И в конце, при связывании ключа с правилом, мы вначале проверяем, если ключ в словаре не существует, то добавляем первое правило в виде списка. Иначе, при существовании ключа, добавляем в его список очередное правило. Отлично, правила добавляются вместе с вероятностями их выбора. Далее, при генерации маршрута черепашки, нужно выбирать эти правила с указанной вероятностью. Переходим в метод generate_path() и также делаем итерации по правилам. Но, теперь с каждым ключом связан список правил rules. Чтобы выбирать их случаным образом для каждой команды, отбор будем делать в методе update_param_cmd(). Поэтому сохраняем список в свойстве self.rules_key и вызываем функцию sub для проведения всех замен текущего ключа. Для этого мы обращаемся к его шаблону rules[0][1] для регулярного выражения: def generate_path(self, n_iter): for n in range(n_iter): for key, rules in self.rules.items(): self.rules_key = rules self.state = re.sub(rules[0][1], self.update_param_cmd, self.state) self.rules_key = None self.state = self.state.upper() Само же свойство self.rules_key добавим в конструктор класса с начальным значением None: self.rules_key = None Давайте теперь переделаем метод update_param_cmd(), чтобы он выбирал и применял правила в соответствии с указанными вероятностями. def update_param_cmd(self, m): if not self.rules_key: return "" rule = self.rules_key[0] if len(self.rules_key) == 1 else self.get_random_rule(self.rules_key) if isinstance(rule[0], str): return rule[0].lower() else: args = list(map(float, m.groups())) return rule[0](*args).lower() Вначале мы проверяем, есть ли вообще список правил и если его не существует, то возврашаем пустую строку. При наличии списка переменная rule будет ссылаться на первый элемент, если длина списка равна единице (то есть, имеем одно правило и отбирать попросту нечего). Иначе вызываем метод get_random_rule() для случайного выбора правила. Этот метод мы определим чуть позже. Далее идет проверка, что содержит правило строку или функцию. Если строку, то возвращаем ее в нижнем регистре. Иначе формируем список аргументов и вызываем функцию с этими параметрами. Осталось определить новый метод get_random_rule(). Он выглядит следующим образом: def get_random_rule(self, rules): p = random.random() # случайное вещественное число в интервале [0; 1] off = 0 for v in rules: if p < (v[2]+off): return v off += v[2] return rules[0] Как здесь происходит отбор правил по их вероятностям? Вначале генерируется случайное значение p с равномерным законом распределения. То есть, p с равной вероятностью может принимать любое значение в интервале от 0 до 1:
Затем, в цикле мы перебираем правила и для каждого из них смотрим, если текущее значение p меньше заданной вероятности срабатывания правила, то выбираем это правило и процесс завершается. Если же условие оказалось ложным, то есть, p больше вероятности выбора текущего правила, то к вероятности следующего правила добавляем вероятность предыдущего с помощью переменной off и процесс сравнения повторяется. В результате, последнее правило со значением суммарной вероятности 1 будет обязательно выбрано, т.к. p не превышает единицы.
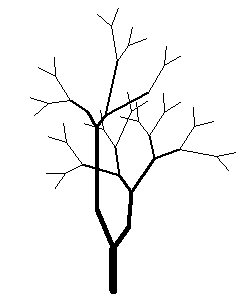
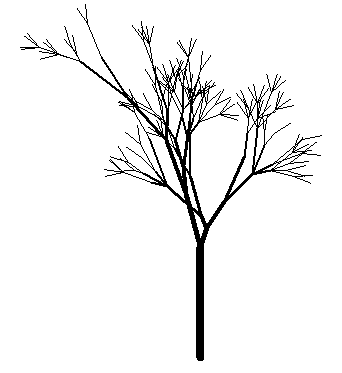
Все, теперь на каждой итерации мы будем получать более разнообразные деревья, так как некоторые разветвления будут отсутствовать. Давайте для эксперимента добавим для символа A еще одно правило: l_sys.add_rules(("A", f"F(1, 1)[+({angle})A][-({angle})A]", 0.5), ("A", f"F(1, 1)[++({angle})A][+({angle})A][-({angle})A][--({angle})A]", 0.4), ("A", f"F(1, 1)[+({angle})O][-({angle})A]", 0.05), ("A", f"F(1, 1)[+({angle})A][-({angle})O]", 0.05), ("F(x, y)", lambda x, y: f"F({(1.2+random.triangular(-0.5, 0.5, random.gauss(0, 1)))*x}, {1.4*y})"), ("+(x)", lambda x: f"+({x + random.triangular(-10, 10, random.gauss(0, 2))})"), ("-(x)", lambda x: f"-({x + random.triangular(-10, 10, random.gauss(0, 2))})"), ) А угол зададим в 15 градусов: angle = 15 У нас получатся еще более интересные решения:
Вот так, благодаря использованию случайных зачений в параметрах и случайному выбору правил можно формировать более живописные изображения фрактальных кривых живой природы. Видео по теме |
. Понятно,
что в нашей L-системе его
нужно ограничивать некоторым разумным диапазоном значений. К счастью, язык Python был разработан
для инженерных задач и математика в нем на высоте. Реализовать генерацию
нормальных СВ можно с помощью функции:
-
вероятности выбора определенного правила. Причем, в сумме эти вероятности
должны быть равны единице:
