|
Добавляем параметры в L-системуАрхив проекта: 6_fractals.py На этом занятии мы с вами сделаем заметное улучшение L-системы, созданной на предыдущих занятиях – добавим в нее параметры. О чем здесь речь и что это за параметры? Смотрите, когда мы с вами рассматривали ветвления и строили фрактальное дерево с аксиомой: axiom = "A" и правилами: l_sys.add_rules(("F", "FF"), ("A", "F[+A][-A]"))
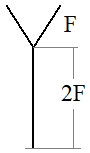
Ветки на каждой новой итерации увеличивались в два раза. И это было много. Было бы правильнее здесь использовать множитель, например, 1,5, то есть, рост был бы в полтора раза, а не в два. Текущей L-системой делать такие манипуляции проблематично. И вот здесь нам на помощь приходят параметры. Было бы хорошо использовать значение, указывающее длину линии рисования. Например, команда: F(1) означала бы рисование линии заданной длины (то есть, без изменений), а команда: F(1.5) рисование линии полуторной длины. И так далее. То есть, указывая после команды в круглых скобках параметр (или несколько параметров), можно существенно улучшить работу L-системы и разнообразить генерируемые фрактальные кривые. Например, для рисования нашего дерева, можно было бы записать правила в виде: A
→ F(1)[+A][-A]
Давайте добавим такой функционал в наш класс. И чтобы сильно не усложнять процесс, я сделаю несколько очевидных ограничений:
В большинстве случаев эти ограничения могут быть легко выполнены. Реализация, которую я приведу, скорее, соответствует учебному примеру, чем реальному проекту. С точки зрения скорости выполнения программу, конечно же можно оптимизировать. Но я решил в ущерб скорости сохранить ясность написания кода и существенно не переделывать программу, написанную на предыдущих занятиях. Как и прежде, будем полагать, что команды записываются в строке и если у них имеются параметры, то они записываются в круглых скобках через запятую: "F(1)+F(2)+F(3)" В данном примере первый параметр увеличивается на 1 на каждой итерации. Давайте вначале реализуем такой функционал в нашей L-системе. Для этого пропишем аксиому вот в таком виде: axiom = "F(1)+A(1)" а правило изменения параметра я опишу с использованием лямбда-функции, следующим образом: l_sys.add_rules(("A(x)", lambda x: f"F({x+1})+A({x+1})")) Смотрите, мы здесь записали команду A(x) в обобщенном виде, где x – это любое число (целое или вещественное), которое может быть записано в круглых скобках сразу после заглавной буквы A. Соответственно, лямбда-функция тоже имеет один параметр (я его обозначил через x, хотя можно определить и любым другим именем). Далее, через двоеточие указываем, что должна возвращать эта функция, когда встретится команда A с параметром. В данном случае, будет возвращена строка со значением параметра x+1. Таким образом, на каждой итерации мы будем получать новую команду F с увеличенным на единицу предыдущим значением. Теперь нам нужно «научить» L-систему понимать такие параметаризированные команды. Для этого я воспользуюсь модулем import re для обработки строк с помощью регулярных выражений. Если вы не знаете что это такое и как им пользоваться, то на этом канале есть курс по регулярным выражениям: https://www.youtube.com/watch?v=1SWGdyVwN3E&list=PLA0M1Bcd0w8w8gtWzf9YkfAxFCgDb09pA В частности, я сделаю следующее. Команды у правил, записанные в виде: F(x) F(x, y) AX(a, b) XY(c, d, e) преобразуем к виду регулярного шаблона: F(x) → F\(([-+]?\b\d+(?:\.\d+)?\b)\)
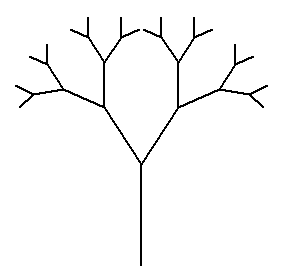
Здесь фрагмент ([-+]?\b\d+(?:\.\d+)?\b) позволяет выделять из строки любое целое или вещетсвенное число. Поэтому преобразованные ключи правил можно применять для поиска соответствующих параметаризированных команд. Именно это мы сделаем в методе add_rules() класса LSystem2D: def add_rules(self, *rules): for key, value in rules: key_re = "" # шаблон регулярного выражения для выделения ключа if not isinstance(value, str): # ключ с параметрами key_re = key.replace("(", r"\(") key_re = key_re.replace(")", r"\)") key_re = re.sub(r"([a-z]+)([, ]*)", lambda m: r"([-+]?\b\d+(?:\.\d+)?\b)" + m.group(2), key_re) self.key_re_list.append(key_re) self.rules[key] = (value, key_re) Здесь вначале идет проверка, если значение не является строкой, значит, это функция, а ключ имеет один или несколько параметров. Далее, мы преобразовываем ключ в шаблон для выделения соответствующей параметаризованной команды и добавляем его в список шаблонов, который нам понадобится позже. Затем, в словаре rules по исходному ключу key сохраняем кортеж со значением ключа и его шаблоном (если команда без параметров, то шаблон будет пустой строкой). В результате, метод add_rules() будет работать как с обычными командами, так и с параметаризированными. Разумеется, свойство key_re_list нужно прописать при создании экземпляра L-системы: self.key_re_list = [] # список шаблонов команд Следующим шагом перепишем метод generate_path() с учетом параметров: def generate_path(self, n_iter): for n in range(n_iter): for key, values in self.rules.items(): if isinstance(values[0], str): self.state = self.state.replace(key, values[0].lower()) else: # команда с параметром self.function_key = values[0] # ссылка на лямбда-функцию self.state = re.sub(values[1], self.update_param_cmd, self.state) self.function_key = None self.state = self.state.upper() Здесь мы смотрим, если команда без параметров, то делаем прежнюю замену, а для параметаризованных команд делаем замену с вызовом лямбда-функции. Для этого используется дополнительная функция update_param_cmd(), которая вначале формирует список параметров в виде вещественных чисел, а затем, вызывает лямбда-функцию с этими параметрами: def update_param_cmd(self, m): if not self.function_key: return "" args = list(map(float, m.groups())) return self.function_key(*args).lower() Мы здесь предполагаем, что лямбда-функции всегда возвращают строку, поэтому в конце стоит вызов метода lower() – перевод в нижний регистр. Кроме того, пропишем свойство function_key в конструкторе класса: self.function_key = None Как вы уже догадались, через него мы вызываем нужную лямбда-функцию. Давайте посмотрим, что у нас получилось. На данный момент L-система должна уметь обрабатывать параметры и формировать параметаризованный маршрут для черепашки. Учитывая нашу аксиому и правило, после первой итерации получим набор команд в виде строки: "F(1)+F(2.0)+A(2.0)" Отлично, то что нужно. Увеличим число итераций до четырех и в консоли появится уже следующая строка: "F(1)+F(2.0)+F(3.0)+F(4.0)+F(5.0)+A(5.0)" Все как надо. Причем, наша L-система может обрабатывать произвольное число параметров у команд. Например, можно задать аксиому в виде: axiom = "F(1, 2)+A(1, 2)" и правило для ее преобразования: l_sys.add_rules(("A(a, b)", lambda x, y: f"F({x+1}, {1.5*y})+A({x+1}, {1.5*y})")) Я здесь намеренно параметры указал через символы a и b, а у лямбда-функции – через x, y, показывая тем самым, что имена параметров у конмад и функции могут быть разными, главное их последовательность. После четырех итераций мы увидим строку: "F(1, 2)+F(2.0, 3.0)+F(3.0, 4.5)+F(4.0, 6.75)+F(5.0, 10.125)+A(5.0, 10.125)" Здорово, да!? Осталось научить черепашку исполнять эти параметаризованные инструкции. Для этого мы перейдем в метод draw_turtle() и первым делом сформируем список шаблонов для выделения команд из строки: key_list_re = "|".join(self.key_re_list) Зачем нужен этот шаблон? Сейчас увидите. Ниже вместо цикла по отдельным символам, мы будем делать цикл по отдельным командам: for values in re.finditer(r"(" + key_list_re + r"|.)", self.state): Этим мне нравится язык Python – здесь все делается относительно просто и красиво. Метод finditer() модуля re возвращает итератор для перебора команд из строки self.state и текущая команда попадает в переменную values. Но values – это объект Match, а не строка, поэтому нам в цикле нужно взять выделенный фрагмент строки с помощью метода group(): cmd = values.group(0) А дальше сделаем так. Если символ F содержится в выделенной команде, то мы пытаемся сформировать список аргументов. При наличии параметров вызываем метод черепашки forward, умножая на значение первого аргумента: if 'F' in cmd: args = [float(x) for x in values.groups()[1:] if x] if len(args) > 0: self.t.forward(self.length*args[0]) else: self.t.forward(self.length) Иначе, выполняем прежнюю команду. Остальные команды пока оставим в прежнем виде. У вас здесь может возникнуть вопрос. Почему именно первый параметр команды F умножается на длину, то есть, отвечает за длину маршрута рисования? Да, в общем то, не почему. Просто я так решил. Пусть первый параметр у F отвечает за длину. Смыслом параметры мы наполняем сами – как решим, так черепашка и будет их обрабатывать. В данном случае, первый параметр – это длина линии. В ваших параметрических L-системах это может быть по другому. Итак, давайте теперь с помощью этой системы нарисуем фрактальное дерево. В качестве начальной аксиомы выберем строку: axiom = "A" а правила пропишем, следующим образом: l_sys.add_rules(("A", "F(1)[+A][-A]"), ("F(x)", lambda x: f"F({1.5*x})")) l_sys.generate_path(5) После выполнения увидим следующее изображение:
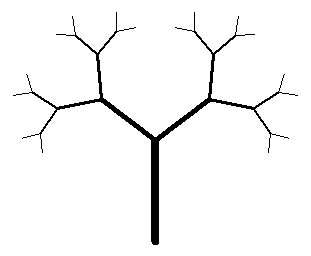
На мой взгляд, дерево получилось естественнее, чем на предыдущем занятии. Здесь соотношение размера свола и веток ближе к реальным деревьям. И все благодаря использованию параметра команды F. В заключение этого занятия я сделаю небольшое улучшение программы. В частности, вынесу из класса LSystem2D логику обработки параметров, так как для разных фракталов она может существенно меняться и прописывать ее жестко в классе L-системы это, очевидно, неправильный подход. Вначале, в конструкторе класса я добавлю словарь, связывающий команду с функцией, которую следует выполнить: self.cmd_functions = {} # словарь связей параметаризованных команд и функций И пропишу еще один метод, который будет добавлять функции к соответствующей команде: def add_rules_move(self, *moves): for key, func in moves: self.cmd_functions[key] = func Как пользоваться этой функцией? Например, в нашем случае можно связать команду F с пользовательской функцией, следующим образом: l_sys.add_rules_move(("F", cmd_turtle_fd)) Мы передаем кортеж, первый элемент – это команда черепашки, а второй – ссылка на функцию, которую следует выполнить для параметаризованной команды. Саму же функцию мы определяем отдельно от класса L-системы, например, так: # список функций для управления параметаризированными командами # у всех функций будет префикс cmd_ и первый параметр t - черепашка def cmd_turtle_fd(t, length, *args): t.fd(length*args[0]) А в методе draw_turtle() в цикле пропишем следующее: def draw_turtle(self, start_pos, start_angle): # *************** turtle.tracer(1, 0) # форсажный режим для черепашки self.t.up() # черепашка воспаряет над поверхностью (чтобы не было следа) self.t.setpos(start_pos) # начальная стартовая позиция self.t.seth(start_angle) # начальный угол поворота self.t.down() # черепашка опускается на "грешную землю" turtle_stack = [] key_list_re = "|".join(self.key_re_list) # *************** # for move in self.state: for values in re.finditer(r"(" + key_list_re + r"|.)", self.state): cmd = values.group(0) args = [float(x) for x in values.groups()[1:] if x] if 'F' in cmd: if len(args) > 0 and self.cmd_functions.get('F'): self.cmd_functions['F'](t, self.length, *args) else: self.t.fd(self.length) elif 'S' in cmd: if len(args) > 0 and self.cmd_functions.get('S'): self.cmd_functions['S'](t, self.length, *args) else: self.t.up() self.t.forward(self.length) self.t.down() elif '+' in cmd: if len(args) > 0 and self.cmd_functions.get('+'): self.cmd_functions['+'](t, self.angle, *args) else: self.t.left(self.angle) elif '-' in cmd: if len(args) > 0 and self.cmd_functions.get('-'): self.cmd_functions['-'](t, self.angle, *args) else: self.t.right(self.angle) elif "[" in cmd: turtle_stack.append((self.t.xcor(), self.t.ycor(), self.t.heading(), self.t.pensize())) elif "]" in cmd: xcor, ycor, head, w = turtle_stack.pop() self.set_turtle((xcor, ycor, head)) self.width = w self.t.pensize(self.width) turtle.done() # чтобы окно не закрывалось после отрисовки То есть, мы здесь при обнаружении параметров у команды, пытаемся вызвать связанную с ней пользовательскую функцию. Если же она не находится или команда без параметров, то отрабатывается стандартное поведение черепашки. Теперь у нас обработка параметров и базовая реализация L-системы разделены между собой. Давайте для еще одного примера добавим второй параметр у команды F, отвечающий за толщину линии рисования: F(<длина линии>, <толщина линии>) и параметр у команд поворота налево и направо, влияющий на изменение угла поворота: +(<множитель угла поворота>) Для этого аксиому оставим прежней, а набор правил и функций, будут следующими: l_sys.add_rules(("A", "F(1, 1)[+(1)A][-(1)A]"), ("F(x, y)", lambda x, y: f"F({1.5*x}, {1.7*y})"), ("+(x)", lambda x: f"+({1.1*x})"), ("-(x)", lambda x: f"-({1.1*x})"), ) l_sys.add_rules_move(("F", cmd_turtle_fd), ("+", cmd_turtle_left), ("-", cmd_turtle_right)) А функции запишем в виде: def cmd_turtle_fd(t, length, *args): t.pensize(args[1]) t.fd(length*args[0]) def cmd_turtle_left(t, angle, *args): t.left(angle * args[0]) def cmd_turtle_right(t, angle, *args): t.right(angle * args[0]) Однако, сейчас, при запуске программы мы увидим ошибку, так как регулярные выражения ожидают в качестве команд символы латинского алфавита. А символы + и - нужно дполнительно экранировать в регулярных выражениях. Для этого в методе add_rules() пропишем дву строчки: key_re = key_re.replace("+", r"\+") key_re = key_re.replace("-", r"\-") После запуска увидим следующее изображение фрактального дерева:
Наш фрактал стал еще ближе к реальным природным объектам. На этом мы завершин наше объемное занятие. Весь код будет выложен на гитхаб, где вы сможете подробно его изучить. Видео по теме |