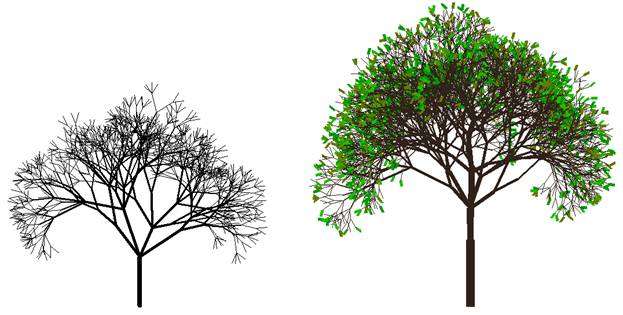
Добавляем цвет в L-систему

Архив проекта: 8_fractals.zip

На этом занятии мы с вами добавим цвет линиям, воспроизводимых L-системой и получим, наконец-то, цветные фрактальные изображения.

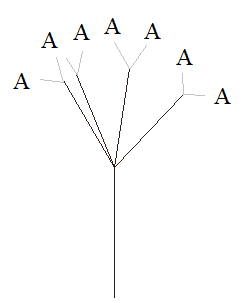
Сразу отмечу, что раскраску универсально сделать нельзя – цвета подбираются индивидуально под каждый класс изображений. Если это деревья – одни цвета, если реки – другие, горы – третьи и так далее. Также здесь дополнительно могут быть использованы элементы изобразительного искусства. Например, при генерации деревьев отдельно прорисовываются листья, которые непосредственно к фрактальной кривой (веткам) не имеют прямого отношения. Но дерево без листьев смотрится не очень красиво, поэтому мы их дополнительно прорисуем.

В принципе, наша L-система уже готова воспроизводить цвета. Точнее, не она сама, а функции рисования cmd_turtle_fd(), cmd_turtle_left(), cmd_turtle_right(). Если в функции cmd_turtle_fd() прописать коричневый цвет линии рисования:

def cmd_turtle_fd(t, length, *args):
    t.pencolor('#30221A')
    t.pensize(args[1])
    t.fd(length*args[0])

То получим дерево с коричневым стволом. Как видите, все предельно просто.

Далее, прорисуем листья. В какой функции нам это сделать? Смотрите, при рисовании ствола дерева на самых верхушках остаются символы A:

Если мы определим функцию для рисования этого символа, то сможем нарисовать его листья. Конечно, у нас так получилось именно для этого фрактала. У других с другими аксиомами и правилами будут другие распределения символов и их художественную обработку нужно будет делать иначе. Поэтому процесс раскраски и визуального оформления фракталов – сугубо индивидуален. Здесь я лишь демонстрирую принцип, но не общее правило.

Итак, в данном случае нам нужно определить функцию для отрисовки символа A. Пропишем ее в списке кортежей функций:

l_sys.add_rules_move(("F", cmd_turtle_fd), ("+", cmd_turtle_left), ("-", cmd_turtle_right), ("A", cmd_turtle_leaf))

И объявим выше в нашей программе:

def cmd_turtle_leaf(t, length, *args):
    if random.random() > 0.5:       # вероятность рисования листа
        return 
 
    p = t.pensize()
    t.pensize(5)
    p = random.randint(0, 2)
    if p == 0:
        t.pencolor('#009900')
    elif p == 1:
        t.pencolor('#667900')
    else:
        t.pencolor('#20BB00')
 
    t.fd(length//2)
    t.pencolor('#000000')
    t.pensize(p)

То есть, мы рисуем листья как отрезок толщиной в 5 пикселей. Причем, цвет выбираем случайным образом один из трех, чтобы листья не сливались друг с другом в кроне дерева.

Но если сейчас запустить программу, то ничего не произойдет. Мы с вами в самой L-системе не обрабатываем символ A. Добавим это в метод draw_turtle():

elif 'A' in cmd:
        if self.cmd_functions.get('A'):
            self.cmd_functions['A'](self.t, self.length, *args)

Теперь дерево выглядит так:

Как видите, все достаточно просто. Вы легко сможете сделать свое оформление: другие цвета, другую форму листьев, изменение цвета ствола в зависимости от номера итерации и прочее. Я вам показал лишь принцип, а дальше дело за вами.

L-система и Pygame

Во второй части этого занятия я сделаю перенос черепашки в Pygame и разделю программу на отдельные модули для удобства работы. У нас будет два основных модуля:

модуль черепашки для Pygame;
модуль L-системы.

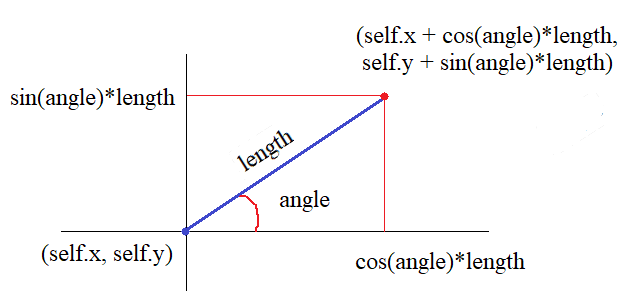
Начнем с модуля черепашки. Она должна уметь выполнять команды, используемой нашей L-системой. Фактически, она должна уметь идти вперед и поворачивать влево и вправо на указанный угол. Остальные команды достаточно очевидны и просты.

Будем полагать, что в классе новой черепашки TurtlePygame будет ссылка на поверхность surf, где черепашка оставляет свой след (рисует), а также ее координаты (x, y), текущий угол angle, толщина рисования линии penwidth, цвет линии color и флаг рисования fl_draw:

class TurtlePygame:
    def __init__(self, surf):
        self.surf = surf
        self.x = 0
        self.y = 0
        self.angle = 0
        self.penwidth = 1
        self.color = (0, 0, 0)
        self.fl_draw = True

Самое главное здесь – это реализовать команду forward(). У меня она выглядит так:

    def forward(self, length):
        x = self.x + length * math.cos(math.radians(self.angle))
        y = self.y - length * math.sin(math.radians(self.angle))
        if self.fl_draw:
            pygame.draw.line(self.surf, self.color, (round(self.x), round(self.y)), (round(x), round(y)), round(self.penwidth))
        self.x = x
        self.y = y

Смотрите, здесь angle – это абсолютный угол поворота черепашки, а self.x, self.y – ее текущие координаты. Значит, чтобы пройти вперед на величину length, нужно выполнить следующие математические преобразования:

Но, так как ось Oy в Pygame направлена вниз, то синус вычитается из текущей координаты. Получаем новую точку (x, y), в которую перемещаем черепашку. После этого координаты self.x, self.y обновляем.

Как видите, все достаточно просто – школьный уровень математики. Соответственно, повороты влево и вправо можно прописать как изменение абсолютного угла:

    def left(self, an):
        self.angle += an
 
    def right(self, an):
        self.angle -= an

Остальные методы черепашки выполняют настолько простые операции, что я их отдельно оговаривать не буду. Все это подробно вы сможете посмотреть в исходниках, которые я выложу на гитхаб.

Итак, черепашка готова. Переходим ко второму модулю – L-системе. Я просто скопировал класс LSystem2D, который мы с вами разработали на предыдущих занятиях. И только в методе draw_turtle() вместо turtle использовал ссылку на новую черепашку self.t.

Все, модули готовы и давайте воспользуемся ими, чтобы в Pygame нарисовать фрактальное дерево. Для этого я уже создал отдельный файл и импортировал эти модули. Далее, идет список функций для отрисовки команд, инициализация Pygame и L-системы. Затем, в главном цикле отрисовываем дерево на разных уровнях итераций. И видим, как оно разрастается.

Вот мы с вами за несколько занятий сделали довольно итересный вариант параметрической и стохастической L-системы и научились рисовать в цвете фрактальное дерево. Конечно, этот вариант L-системы – лишь учебный пример. Здесь много чего можно улучшить, если сразу поставить цель реализации параметрической L-системы со случайным поведением. Я же использовал наследие прошлых занятий и это сказалось на качестве кода. Поэтому в качестве задания попробуйте самостоятельно написать универсальный класс L-системы, делающая все те же самые вещи. Также попробуйте оформить в цвете другие фракталы, например, кустики или нарисовать фрактальные цветы. В общем, тут богатое поле для творчества. Ну а основные моменты построения L-систем, я думаю, вы теперь знаете.

Добавляем цвет в L-систему

L-система и Pygame

Видео по теме