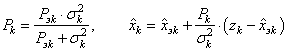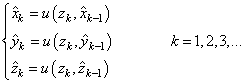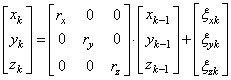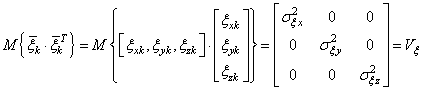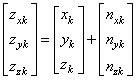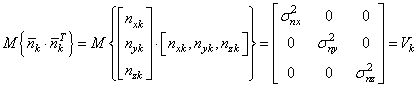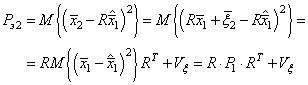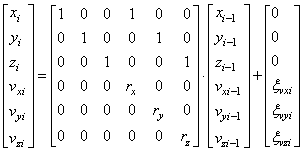Векторный фильтр Калмана

Реализация алгоритма на Python (lesson 7. kalman_vector_1.py)

На предыдущем занятии мы увидели как можно применить фильтр Калмана для построения оценок координаты x при перемещении мальчика. Он выглядел так:

Но, если рассмотреть более общую задачу и попытаться построить оценки сразу по трем пространственным осям, то в самом простом случае можно выполнить три таких процедуры независимо по каждой оси:

Здесь  - это калмановский алгоритм построения текущей оценки. И, так как все эти три координаты представляют собой точку в трехмерном пространстве, то изменение положение объекта удобнее представить векторно-матричной марковской моделью:

или, в таких очевидных обозначениях:

Здесь и далее будем полагать, что все случайные составляющие подчиняются нормальному закону распределения с нулевым средним и некоторыми дисперсиями. Например, для

Модель наблюдений, соответственно, определим вектором z:

или, в векторном виде:

Здесь также дисперсии шумов, будут образовывать диагональную матрицу:

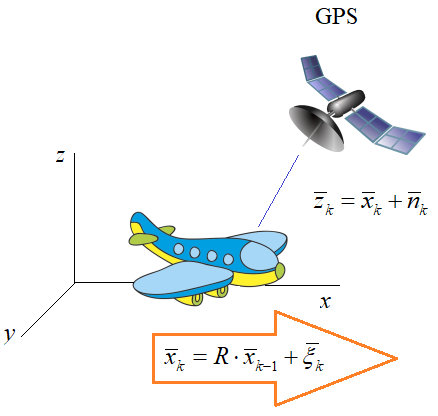
Таким образом, у нас есть векторная марковская модель изменения объекта в пространстве и вектор наблюдений текущего местоположения объекта:

Когда на вход приемника приходит самое первое наблюдение, то лучшая оценка – это значение самого наблюдения:

с дисперсией ошибок оценивания:

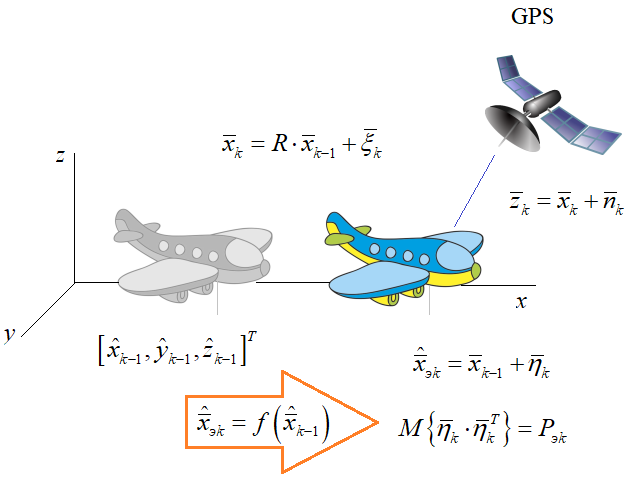
В следующий момент времени самолет немного меняет свое местоположение и на вход GPS-приемника приходит очередное наблюдение:

Как в этой ситуации нам построить оценку текущего местоположения? Одно наблюдение у нас есть – это вектор . Второе можно взять как прогноз текущего положения из предыдущей оценки , используя марковскую модель движения:

Я не буду здесь приводить доказательство оптимальности этого прогноза, вывод делается аналогично одномерному случаю, о котором мы говорили на предыдущем занятии.

Теперь, нам нужно вычислить дисперсию ошибок прогноза, которая равна:

В результате, мы имеем все необходимые данные для построения оценок координат на текущем шаге с помощью векторного фильтра Калмана. Используя формулы скалярного фильтра:

Обобщим их для векторно-матричного случая:

Как видите, мы здесь лишь формально преобразовали скалярные выражения в векторные и получили возможность строить уже векторы оценок. Это очень удобно. В этом одно из достоинств векторов и матриц: они позволяют легко обобщать задачи на многомерный случай.

Итак, на втором шаге, имеем следующие вычисления:

Ну а все последующие положения рекуррентно вычисляются по этим же самым формулам.

Давайте реализуем векторный фильтр Калмана на Python и посмотрим на результаты его работы.

Делаем

Фактически, при условии некоррелированности шумов и независимости перемещений по каждой из координат, мы получили три независимых канала оценивания параметров x, y, z:

Однако, если модифицировать нашу модель и учесть в ней скорости движения объекта по каждой из координат:

То у нас будет связь между наблюдениями скорости и соответствующей координаты. Причем, векторный фильтр Каламана автоматически наилучшим образом скомбинирует эти набюлдения для вычисления оптимальной выходной оценки в соответствии с описанной моделью перемещения. И это очень удобно. Нам не нужно решать систему линейных уравнений, находить оптимальные коэффициенты, все аккуратно расписывать. Все это делается автоматически при вычислении обратных матриц в фильтре Калмана.

Далее, для нашего второго варианта матрицы дисперсий порождающего шума и шума наблюдений, будут выглядеть так:

А весь остальной алгоритм оценивания будет прежним:

Мало того, если шумы в наблюдениях коррелированны между собой, то это приведет лишь к изменению начальной записи этих матриц, реализация фильтра Калмана на уровне векторов и матриц останется прежней. Вот так можно описать и реализовать общий алгоритм оценивания, для разных моделей движения объектов и шумов в наблюдениях.

Видео по теме

#1: Метод наименьших квадратов

#2: Метод градиентного спуска

#3: Метод градиентного спуска для двух параметров

#4: Марковские процессы в дискретном времени

#5: Фильтр Калмана дискретного времени

#6: Фильтр Калмана для авторегрессионого уравнения

#7: Векторный фильтр Калмана

#8: Фильтр Винера

#9: Байесовское построение оценок, метод максимального правдоподобия

#10: Байесовский классификатор, отношение правдоподобия