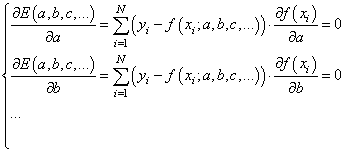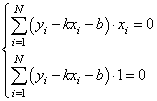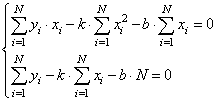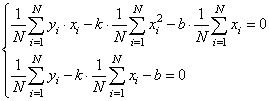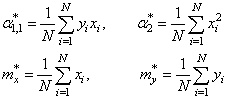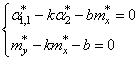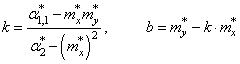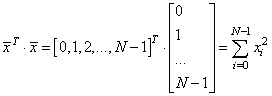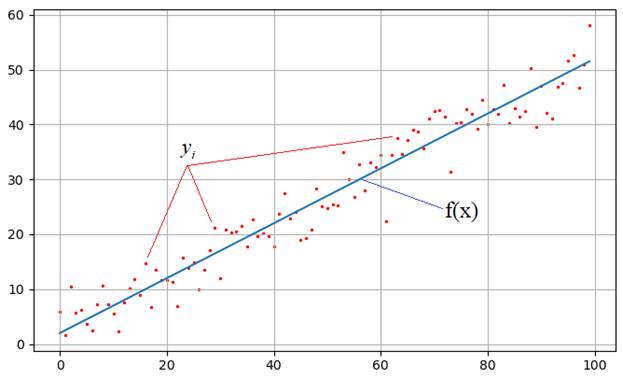
|
Метод наименьших квадратовНа этом занятии мы с вами рассмотрим алгоритм, который носит название метод наименьших квадратов. Для начала немного теории. Чтобы ее хорошо понимать нужны базовые знания по теории вероятностей, в частности понимание ПРВ, а также знать, что такое производная и как она вычисляется. Остальное я сейчас расскажу. На практике встречаются задачи, когда производились измерения некоторой функциональной зависимости, но из-за погрешностей приборов, или неточных сведений или еще по какой-либо причине, измерения немного отстоят от истинных значений функции и образуют некий разброс:
Наша задача:
зная характер функциональной зависимости, подобрать ее параметры так, чтобы она
наилучшим образом описывала экспериментальные данные
чтобы построить аппроксимацию (приближение) линейного графика к экспериментальным зависимостям. Конечно, вид функциональной зависимости может быть и другим, например, квадратической (парабола), синусоидальной, или даже определяться суммой известных функций, но для простоты понимания, мы для начала рассмотрим именно линейный график с двумя неизвестными коэффициентами. Итак, будем
считать, что на первый вопрос о характере функциональной зависимости
экспериментальных данных ответ дан. Следующий вопрос: как измерить качество
аппроксимации измерений - сумма квадратов ошибок отклонений:
- сумма модулей ошибок отклонений:
- минимум максимальной по модулю ошибки:
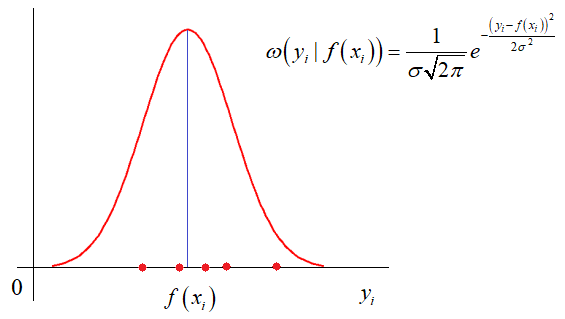
и так далее. Каждый из критериев может приводить к своему алгоритму обработки экспериментальных значений. Так вот, в методе наименьших квадратов используется минимум суммы квадратов ошибок. И этому есть математическое обоснование. Часто результаты реальных измерений имеют стандартное (гауссовское) отклонение относительно измеряемого параметра:
Здесь σ –
стандартное отклонение (СКО) наблюдаемых значений
Получается, что лучшее
описание экспериментальных данных с помощью функции
Здесь также множитель можно не учитывать, получаем критерий качества минимум суммы квадрата ошибок:
Как мы помним,
наша цель – подобрать параметры
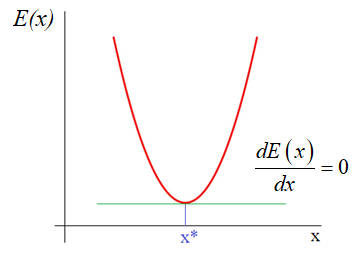
которые как раз и обеспечивают минимум этого критерия, то есть, величина E зависит от этих подбираемых величин:
И ее можно
рассматривать как квадратическую функцию от аргументов
Здесь все также, нужно взять частные производные по каждому параметру и приравнять результат нулю, получим систему линейных уравнений:
Чтобы наполнить конкретикой эту систему, нам нужно вернуться к исходному примеру с линейной функцией:
Эта функция зависит от двух параметров: k и b с частными производными:
Подставляем все в систему, имеем:
или, в виде:
Разделим все на N:
Смотрите, что в итоге получилось. Формулы с суммами представляют собой первые и вторые начальные моменты, а также один смешанный момент:
Здесь * означает экспериментальные моменты. В этих обозначениях, получаем:
Отсюда находим, что
Все, мы получили оценки параметров k и b для линейной аппроксимации экспериментальных данных по методу наименьших квадратов. По аналогии можно вычислять параметры для других функциональных зависимостей, например, квадратической:
Здесь будет уже три свободных параметра и три уравнения, решая которые будем получать лучшую аппроксимацию по критерию минимума суммарной квадратической ошибки отклонений. Реализация на PythonВ заключение этого занятия реализуем метод наименьших квадратов на Python. Для этого нам понадобятся две довольно популярные библиотеки numpy и matplotlib. Если они у вас не установлены, то делается это просто – через команды: pip install numpy pip install matplotlib После этого, мы можем их импортировать и использовать в программе: import numpy as np import matplotlib.pyplot as plt Первая довольно эффективная для выполнения различных математических операций, включая векторные и матричные. Вторая служит для построения графиков. Итак, вначале определим необходимые начальные величины: N = 100 # число экспериментов sigma = 3 # стандартное отклонение наблюдаемых значений k = 0.5 # теоретическое значение параметра k b = 2 # теоретическое значение параметра b Формируем вспомогательный вектор
с помощью метода array, который возвращает объект-вектор на основе итерируемой функции range: x = np.array(range(N)) Затем, вычисляем значения теоретической функции: f = np.array([k*z+b for z in range(N)]) и добавляем к ней случайные отклонения для моделирования результатов наблюдений: y = f + np.random.normal(0, sigma, N) Если сейчас отобразить наборы точек y, то они будут выглядеть следующим образом: plt.scatter(x, y, s=2, c='red') plt.grid(True) plt.show() Теперь у нас все есть для вычисления коэффициентов k и b по экспериментальным данным: # вычисляем коэффициенты mx = x.sum()/N my = y.sum()/N a2 = np.dot(x.T, x)/N a11 = np.dot(x.T, y)/N kk = (a11 - mx*my)/(a2 - mx**2) bb = my - kk*mx Здесь выражение x.T*x – это произведение:
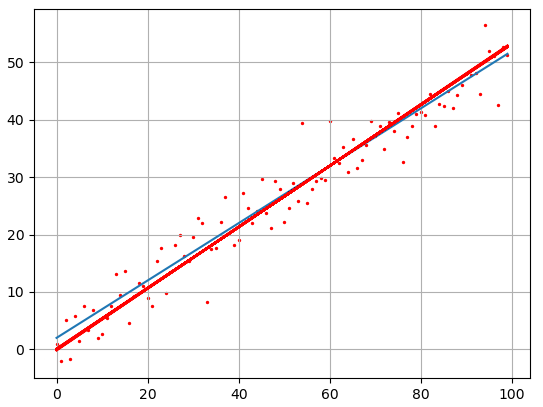
Далее, построим точки полученной аппроксимации: ff = np.array([kk*z+bb for z in range(N)]) и отобразим оба линейных графика: plt.plot(f) plt.plot(ff, c='red')
Как видите результат аппроксимации довольно близок начальному, теоретическому графику. Вот так работает метод наименьших квадратов. Реализация алгоритма на Python (файл mnsq.py) Видео по теме |
Например, на
рисунке явно прослеживается линейная зависимость. Мы это можем определить либо
чисто визуально, либо заранее знать о характере функции. Но, в любом случае
предполагается, что ее общий вид нам известен. Так вот, для линейной функции
достаточно определить два параметра k и b:
? Вообще, таких
критериев можно придумать множество, например:
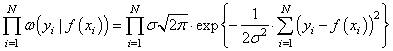
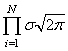, а экспонента будет
принимать максимальное значение при минимуме ее отрицательной степени:
функции
