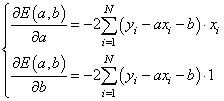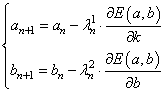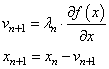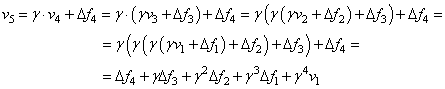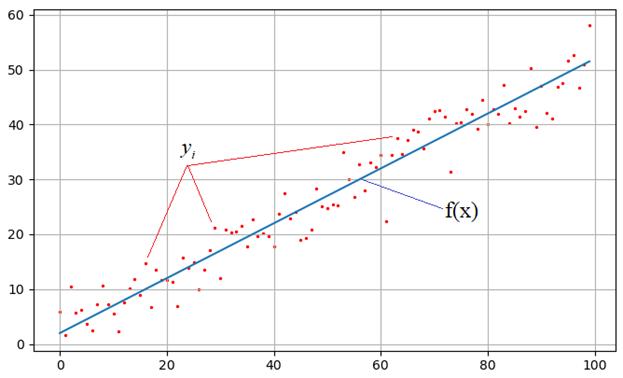
|
Метод градиентного спуска для двух параметровТеперь, когда мы с вами в целом разобрались в работе градиентного алгоритма, давайте применим его к решению задачи поиска оптимальных значений параметров a и b линейной функции:
для аппроксимации
наблюдений
Мы с вами это уже делали методом наименьших квадратов, а теперь сделаем с помощью метода наискорейшего спуска. Критерием качества здесь выступает минимум суммы квадратов ошибок:
Градиент этого функционала определяется частными производными:
А сам алгоритм примет вид:
Здесь Реализация алгоритма на PythonРеализация алгоритма на Python (файл grad2.py) Реализуем этот алгоритм на Python и посмотрим на полученный результат. Вначале подключим необходимые библиотеки: import time import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D И определим три функции: def E(y, a, b): ff = np.array([a * z + b for z in range(N)]) return np.dot((y-ff).T, (y-ff)) def dEda(y, a, b): ff = np.array([a * z + b for z in range(N)]) return -2*np.dot((y - ff).T, range(N)) def dEdb(y, a, b): ff = np.array([a * z + b for z in range(N)]) return -2*(y - ff).sum() Первая функция вычисляет значение ошибки для указанных параметров a, b и набора наблюдений y. Вторая и третья функции возвращают значения частных производных по параметру a и параметру b. Далее мы определяем набор необходимых параметров для работы алгоритмов: N = 100 # число экспериментов Niter = 50 # число итераций sigma = 3 # стандартное отклонение наблюдаемых значений at = 0.5 # теоретическое значение параметра k bt = 2 # теоретическое значение параметра b Начальные значения параметров и шаги сходимости по каждому параметру: aa = 0 bb = 0 lmd1 = 0.000001 lmd2 = 0.0005 Затем, формируем теоретическую прямую и набор наблюдений y: f = np.array([at*z+bt for z in range(N)]) y = np.array(f + np.random.normal(0, sigma, N)) После этого вычисляем вид функции потерь (критерия качества) в небольшом диапазоне параметров a и b: a_plt = np.arange(-1, 2, 0.1) b_plt = np.arange(0, 3, 0.1) E_plt = np.array([[E(y, a, b) for a in a_plt] for b in b_plt]) Это нам нужно будет исключительно с целью визуализации работы алгоритма. Далее, включаем интерактивный режим отображения и формируем трехмерную систему координат: plt.ion() # включение интерактивного режима отображения графиков fig = plt.figure() ax = Axes3D(fig) Отображаем трехмерный график функции потерь и подписываем оси: a, b = np.meshgrid(a_plt, b_plt) ax.plot_surface(a, b, E_plt, color='y', alpha=0.5) ax.set_xlabel('a') ax.set_ylabel('b') ax.set_zlabel('E') Рисуем текущую точку по координатам параметров a и b: point = ax.scatter(aa, bb, E(y, aa, bb), c='red') # отображение точки красным цветом и запускаем процесс градиентного спуска: for n in range(Niter): aa = aa - lmd1 * dEda(y, aa, bb) bb = bb - lmd2 * dEdb(y, aa, bb) ax.scatter(aa, bb, E(y, aa, bb), c='red') # перерисовка графика и задержка на 10 мс fig.canvas.draw() fig.canvas.flush_events() time.sleep(0.01) print(aa, bb) После этого выключаем интерактивный режим и сохраняем отображаемый график на экране: plt.ioff() # выключение интерактивного режима отображения графиков plt.show() Далее, для визуальной проверки качества подбора параметров, отображаем теоретическую прямую и результат найденной аппроксимации: # отображение графиков аппроксимации ff = np.array([aa*z+bb for z in range(N)]) plt.scatter(range(N), y, s=2, c='red') plt.plot(f) plt.plot(ff, c='red') plt.grid(True) plt.show() Как видим, алгоритм вполне справился со своей задачей и в двумерном случае, причем, мы, фактически, разбили задачу на независимый поиск по каждому параметру. Их связка сохранялась только в выражениях частных производных, но сам алгоритм работал независимо по каждой величине. И это его преимущество – практически линейное увеличение вычислительной сложности при увеличении размерности пространства поиска. Сложность строго оптимальных методов растет в геометрической прогрессии и, начиная с определенного момента, уже 1000 параметров они не применимы для большинства практических задач. Именно поэтому градиентный спуск и получил такую широкую популярность и является ключевым при обучении нейронных сетей, где число изменяемых параметров достигает десятков, а то и сотен тысяч. А в ряде случаев и еще больше. Методы оптимизацииИтак, при реализации алгоритма наискорейшего спуска, перед разработчиками встают две важные задачи:
Первая задача решается, преимущественно, выбором нескольких разных начальных приближений подбираемых параметров и последующего отбора лучшего результата. Вторая задача несколько разнообразнее. В рамках наших занятий мы рассматривали варианты постоянного шага:
изменяемого шага:
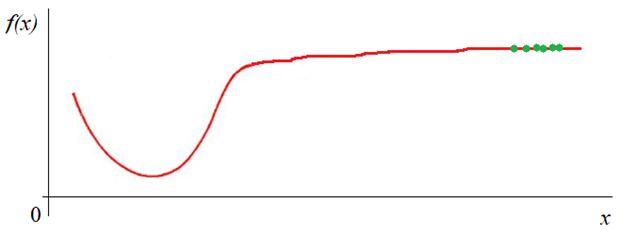
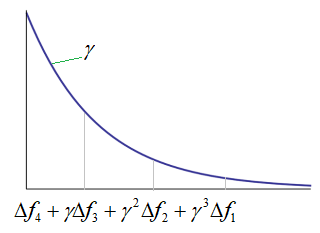
и нормировки градиента. Но это далеко не все известные методы оптимизации. Давайте представим себе, что некая целевая функция имеет следующий вид:
И мы по пологому участку медленно движемся к точке минимума (зеленые точки). То есть, в среднем, имеем однонаправленные градиенты небольших величин:
Простой анализ
нам подсказывает, что для ускорения сходимости нужно в таких ситуациях
увеличивать значения
где
Как это работает?
Если расписать полученные суммы, например, для
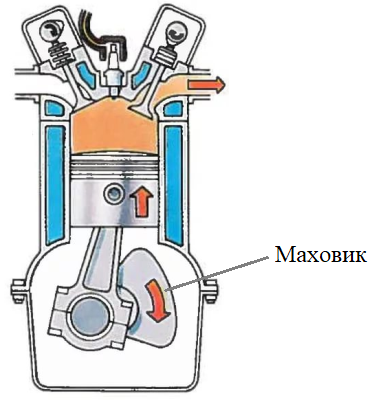
То есть, происходит суммирование градиентов. И, если градиенты преимущественно направлены в одну сторону, то шаг изменения v начинает увеличиваться, следовательно, увеличивается и скорость перемещения по пологому участку графика. Это очень похоже на работу маховика поршневого двигателя: на малых оборотах он обеспечивает более надежный вращательный момент, и двигатель ведет себя более предсказуемо:
Эту же роль маховика в градиентном алгоритме и играет дополнительное слагаемое, обеспечивая в ряде случаев более быструю сходимость. Ускоренные градиенты НестероваРазвитие этой идеи привело к идее оптимизации, известной как «ускоренные градиенты Нестерова», которая часто используется в алгоритмах градиентного спуска при обучении нейронных сетей. Отличие от метода с моментом только в том, что текущее значение градиента берется не в точке текущего значения подбираемого параметра:
а с учетом накопленного смещения:
То есть, мы как бы заглядываем наперед и смотрим какое там значение градиента. Как показал опыт, такой подход, в среднем, повышает скорость сходимости градиентного алгоритма. Существует множество других алгоритмов оптимизации. Работают они по похожим принципам. Я не буду их подробно приводить, лишь перечислю основные из них:
На мой взгляд, все эти и некоторые другие идеи оптимизации, хорошо представлены в статье: https://habr.com/ru/post/318970/ Видео по теме |
.
-
шаги сходимости для параметров a и b соответственно.
.
Один из подходов оптимизации на основе момента предлагает использовать
инерционное слагаемое при вычислении корректирующего слагаемого 
:
обычно
выбирается в районе 0,9 и должно быть в пределах:
,
то получим:
