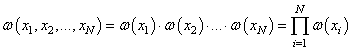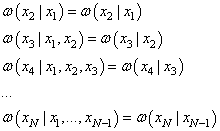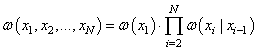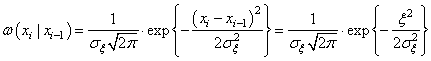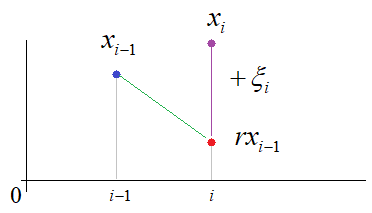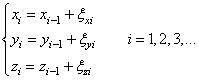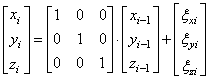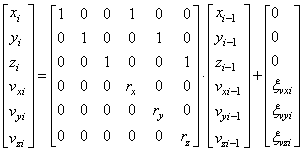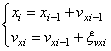|
Марковские процессы в дискретном времениРеализации алгоритмов на Python (файлы lesson 4. markov_1.py и lesson 4. markov_2.py) На этом занятии мы с вами познакомимся с одной довольно распространенной на практике моделью, известной под названиями: марковская последовательность, марковский процесс и т.п. Они были названы в честь русского математика Маркова Андрей Андреевича, который в 1907 году положил начало изучению таких моделей. Давайте посмотрим, чем они так хороши и где применяются.
Из теории вероятностей хорошо известно, что произвольную случайную дискретную последовательность, длиной N отсчетов:
можно в общем виде вероятностно описать с помощью многомерной ПРВ:
Однако, на практике использовать такую формулу очень неудобно, так как она приводит к резкому увеличению сложности алгоритмов при увеличении числа отсчетов N. Как можно было бы ее упростить? Самое простое – это все условные ПРВ заменить безусловными:
Но для каких сигналов корректно применить такую ПРВ? Да, для тех, у которых все отсчеты являются независимыми между собой. Обычно, он соответствует шуму, а не полезному сигналу.
Как же нам описать полезный сигнал, у которого отсчеты зависимы между собой и при этом не усложнять его вероятностное описание? Для этого нужно сделать следующий шаг в усложнении модели и все условные ПРВ сделать зависимыми только от предыдущего момента времени:
И, тогда многомерная ПРВ может быть записана в довольно компактном и простом виде:
Случайные последовательности, удовлетворяющие такой ПРВ, получили название марковские последовательности. Но что это за сигналы, которые она описывает? В самом простом варианте, можно взять такую модель:
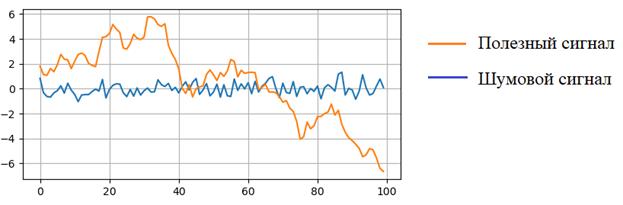
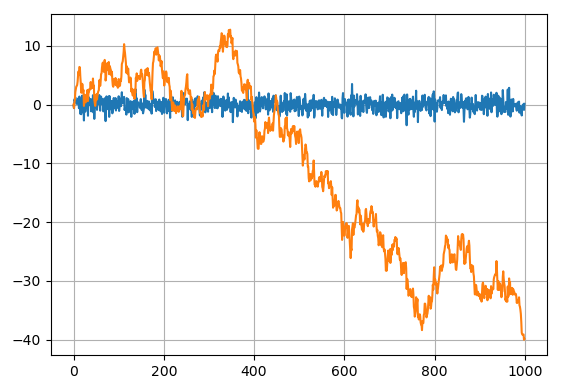
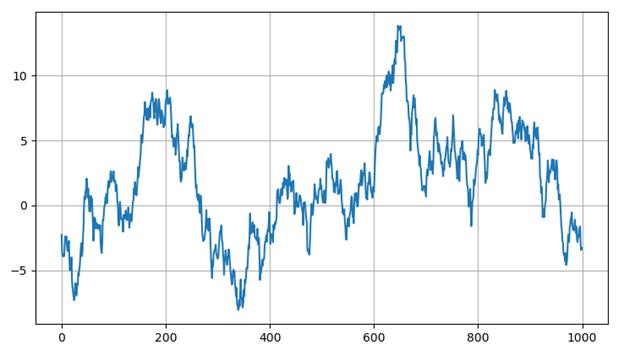
Здесь Реализация на Pythonimport numpy as np import matplotlib.pyplot as plt N = 1000 sigma = 1 fSignal = np.zeros(N) fNoise = np.random.normal(0, sigma, N) for i in range(1, N): fSignal[i] = fSignal[i-1] + fNoise[i] plt.plot(fNoise) plt.plot(fSignal) plt.grid(True) plt.show()
Здесь синий график – это шум, на основе которого была построена простейшая марковская последовательность. Хорошо, визуально мы видим, как он отличается от обычного шумового сигнала, но что он может описывать в реальной жизни? В действительности, очень важный процесс – перемещение объекта в пространстве, например, человека, машины, самолета, корабля и т.д. В частности,
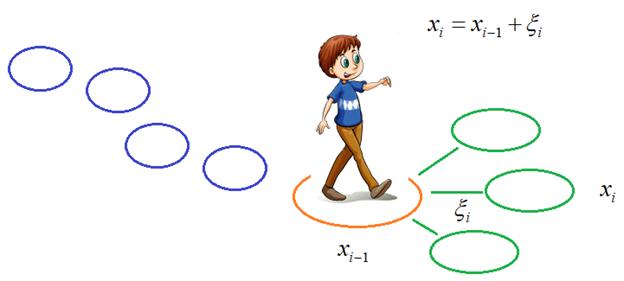
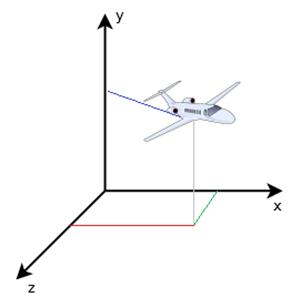
посмотрим на перемещение идущего мальчика. Наша задача спрогнозировать его
положение по оси X в следующий момент времени. Очевидно, для этого не
нужно знать, где он был пять минут назад, достаточно знания его текущего
местоположения (ну, может быть, еще скоростей движения по координатам X и Y и ускорений, но
для простоты мы сейчас это не берем в расчет). В следующий момент времени,
допустим, через секунду, он неизбежно будет где-то поблизости. И это где-то,
как раз и описывается случайной добавкой
Причем, для
этого конкретного случая, когда случайная добавка
Следовательно, модель полностью определена и может быть использована для построения различных алгоритмов, например, навигации или управления. Аналогично будет и для любого другого движущегося в пространстве объекта. Но у этой конкретной модели есть один недостаток: дисперсия случайного процесса будет возрастать с ростом числа наблюдений, так как любое текущее положение – это сумма случайных добавок:
соответственно, дисперсия (с учетом нулевого МО):
Авторегрессия 1-го порядкаКонечно, для описания координат x и y это вполне нормально, но, например, для описания изменения скорости или ускорения – уже не подходит. Но мы можем ее легко модифицировать и адаптировать под свои нужды, например, вот так:
Мы здесь
выбираем коэффициент
уменьшается в
Такая модель получила название авторегрессии 1-го порядка. И выглядит следующим образом: import numpy as np import matplotlib.pyplot as plt N = 1000 sigma = 5 r = 0.99 en = np.sqrt((1-r*r)*sigma*sigma) fSignal = np.zeros(N) fSignal[0] = np.random.normal(0, sigma) for i in range(1, N): fSignal[i] = r*fSignal[i-1] + np.random.normal(0, en) plt.plot(fSignal) plt.grid(True) plt.show()
Векторные марковские последовательностиВернемся к задаче построения модели положения движущегося в пространстве объекта.
Здесь мы имеем три пространственные координаты. И для каждой из координат можно записать модель:
Однако, оперировать на практике такой системой не очень удобно. Гораздо лучше все представить в векторно-матричной форме:
или, в следующих обозначениях:
В результате, мы получаем удобную и компактную векторно-матричную модель марковской последовательности. Причем, ее общий вид останется без изменений, если, например, добавить в нее скорости по каждой из координат:
то получим следующий алгоритм изменения координат:
и так для каждой
координаты. Это более точное описание движения, так как здесь учитываются еще и
скорости. То есть, подбирая случайные добавки Видео по теме |
- это
случайная величина, например, гауссовская с нулевым средним и дисперсией 
. Давайте
построим такую последовательность и посмотрим как она выглядит:
,
который уменьшает предыдущее значение 
, в
результате, дисперсия произведения (для центрированных величин 
):
, следовательно,
чтобы сохранить дисперсию постоянной для всех отсчетов нашей модели, нужно
добавить случайную величину с дисперсией:
можно
строить прогноз положения объекта в следующий момент времени. Например, если
самолет летит по курсу со скоростью 700 км/ч, то его скорость по направлению
движения 
, а,
значит, прогноз, скажем, через одну секунду в соответствии с нашей моделью
будет лежать где-то впереди по оси X. Смещения по другим осям будут
практически равны 0. Конечно, увеличивая временной интервал прогнозирования, мы
будем получать все менее точные значения. Например, через час самолет может уже
приземлиться и исходные данные попросту будут некорректно отражать текущее
положение дел. Но на короткие интервалы можно получать вполне приемлемые
результаты. Кроме того, эта модель показывает нам как можно обрабатывать
данные, т.е. строить алгоритмы, например, для навигации или управления
объектами. Но об этом мы поговорим уже на следующем занятии.
