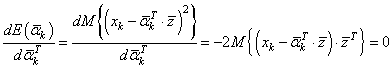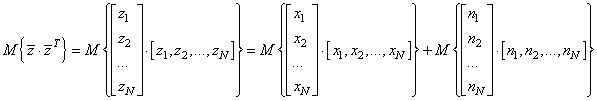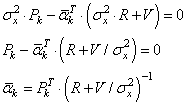|
Фильтр ВинераРеализация алгоритма на Python (lesson 8. Filter Winer.py) На предыдущих занятиях мы с вами рассмотрели принцип построения оценок с помощью фильтра Калмана в различных его вариациях. И отмечали, что он дает минимум среднего квадрата ошибки:
при гауссовских шумах и марковских последовательностях. Но что делать, если случайная последовательность
изменения параметра x не марковская, а шумы остаются гауссовскими? Чтобы было понятнее, давайте предположим, что у нас имеется гауссовский процесс, описывающий изменение массы человека в течение N дней:
и будем полагать, что мы не уверены, что он марковский, но точно гауссовский:
Затем, в одно и то же время каждого дня измеряем вес и фиксируем его с некоторой погрешностью. Получаем наблюдаемые данные:
Шум наблюдения также считаем гауссовским с нулевым средним и известной дисперсией
И ставится
задача: как в таких условиях построить оптимальные оценки
Мы будем полагать, что оценки истинного веса в каждый день определяются, когда уже известны все наблюдения:
Тогда, учитывая гауссовский характер и процесса и шумов, оптимальные оценки можно построить по правилу:
Здесь
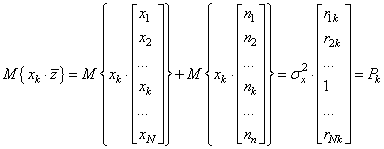
Отбрасываем множитель -2, получаем:
Теперь осталось выяснить, что из себя представляют эти МО. Первое можно расписать так:
Вот эти величины
Здесь при центрировании для простоты понимания материала полагается что мы имеем дело со стационарным процессом, то есть, процесс, у которого МО и дисперсия одинаковы для каждого k-го отсчета. Итак, первое МО – это взаимная корреляция между k-м отсчетом и всеми остальными отсчетами СП. Второе МО можно расписать так:
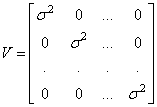
Первое МО представляет собой корреляционную матрицу для СП x:
Второе МО – это такая же корреляция, но для шумов. Полагая шумы некоррелированными между собой, получаем диагональную матрицу:
В этих обозначениях оптимальное значение весовых коэффициентов для построения оценки k-го отсчета, равно:
То есть, чтобы нам определить оптимальные коэффициенты, необходимо знать (помимо дисперсии шума) корреляционную функцию СП x. Но нам ничего не остается как с этим согласиться и вычислять оптимальную оценку по формуле:
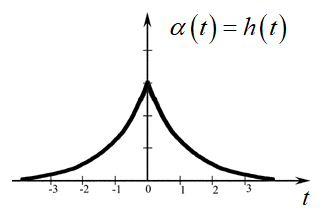
В результате, у нас получилась оценка, построенная в соответствии с идеей фильтра Винера. Нельзя сказать, что это фильтр Винера в чистом виде. Но общий подход соответствует винеровской фильтрации. Если бы мы захотели реализовать строго оптимальный алгоритм как это было предложено самим Робертом Винером, то должны были бы взять бесконечное число наблюдений до k-го отсчета и столько же бесконечно много после. Почему так? Дело в том, что весовые коэффициенты α остаются ненулевыми, сколько бы наблюдений мы ни взяли, а значит, для оптимальной оценки этих наблюдений нужно бесконечно много:
Как вы понимаете, на практике это сделать невозможно, поэтому ограничиваются несколькими ближайшими и превращают оптимальный, но нереализуемый фильтр, в близко-оптимальный (квазиоптимальный), но реализуемый. Что мы и сделали в нашей задаче. Также этот график наглядно показывает отличие работы фильтра Винера от Калмана: при калмановской фильтрации использовалась предыдущая оценка и текущее наблюдение, а при винеровской фильтрации используются все доступные наблюдения для построения текущей оценки. Именно поэтому модель сигнала перестает иметь какое-либо значение, главное чтобы он был гауссовским. Итак, давайте выполним построение оценок для рассматриваемого примера взвешивания человека, полагая (для простоты), что корреляционная функция СП имеет экспоненциальный вид:
где a – коэффициент корреляции между соседними отсчетами, например, 0,9. Вот так, в самом простом варианте реализуется построение оценок с позиции винеровской фильтрации. Видео по теме |