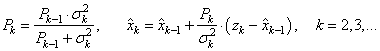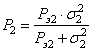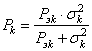Фильтр Калмана для авторегрессионого уравнения

Смотреть материал на видео

На предыдущем занятии мы с вами рассмотрели общий принцип работы фильтра Калмана и получили следующие рекуррентные выражения для построения оценки параметра x – координаты стоящего человека, по наблюдениям :

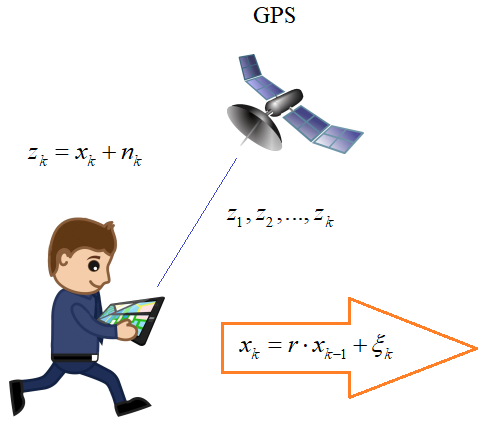
Давайте теперь сделаем следующий шаг и положим, что измерения координаты происходят во время движения:

Причем, модель изменения положения идущего мальчика вдоль оси X будет определяться марковской последовательностью:

Здесь  – некий коэффициент модели (выбирается исходя из конкретной решаемой задачи, например, в нашем случае он может быть равен 0,99 или даже 1, т.е. будем считать, что он известен).  - гауссовские СВ с нулевым МО и дисперсией .

Далее, на вход GPS-приемника поступают наблюдения в дискретные моменты времени (допустим, каждую секунду) в формате:

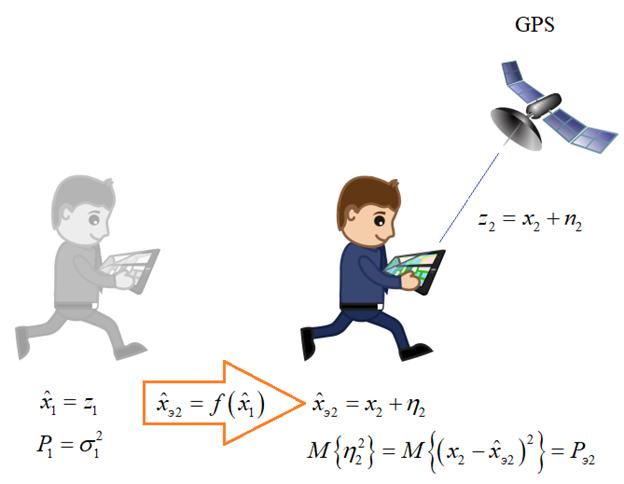
Здесь  - случайные гауссовские величины с нулевым МО и дисперсиями . Наша задача реализовать алгоритм, который бы на основе поступающих наблюдений формировал оценки текущего местоположения по координате X.

Для этого, конечно же, воспользуемся фильтром Калмана. При поступлении первого наблюдения оценка будет равна:

Затем, мальчик немного переместился и на вход GPS-приемника поступило следующее наблюдение:

Как нам теперь правильно применить фильтр Калмана, чтобы использовать ранее полученную оценку  и текущее наблюдение ? Да, нам нужно построить прогноз из предыдущего положения x1 в текущее x2:

Тогда этот прогноз можно воспринимать как второе наблюдение:

с дисперсией ошибки этого прогноза:

И далее уже по фильтру Калмана «взвесить» эти два наблюдения и получить оценку текущего местоположения.

Здесь возникает задача построения прогноза. Для этого мы воспользуемся нашей моделью перемещения мальчика:

в соответствии с которой значение

Затем, учитывая, что все шумы и СВ в моделях подчиняются нормальному закону, то лучший прогноз может быть построен по правилу:

где α – некоторый неизвестный весовой коэффициент. И, как вы уже догадались, найти этот коэффициент можно из условия минимума дисперсии ошибки прогнозирования:

Из уравнения:

легко найти, что

и лучший прогноз есть:

с дисперсией ошибки прогнозирования:

Все, теперь у нас есть вся информация для вычисления оценки  с помощью фильтра Калмана:

где ошибка оценивания второго отсчета координаты X, равна:

По аналогии вычисляются оценки для любого k-го отсчета. Сначала вычисляем прогноз и дисперсию ошибки прогнозирования:

Затем, вычисляем дисперсию ошибки оценивания k-го отсчета:

и, наконец, саму оценку:

Фактически, мы получили алгоритм фильтрации авторегрессионной последовательности 1-го порядка с помощью фильтра Калмана в условиях гауссовского независимого шума.

Важным фактом здесь является построение оптимальных оценок. То есть, никакой другой алгоритм не даст лучших результатов при таких условиях. Что это за условия:

1. Мы работаем с гауссовскими распределениями (сигнал x и шумы в наблюдениях z подчиняются нормальным распределениям).

2. Модель перемещения – марковская. Это значит, что оценка, полученная на предыдущем шаге , содержит всю необходимую информацию для построения оптимальной оценки на текущем шаге .

При других условиях, возможно, этот алгоритм придется корректировать, чтобы он давал оптимальные оценки. Если, это конечно возможно. Нередко бывают ситуации, когда реализовать на практике оптимальный алгоритм невозможно.

Реализация на Python

Реализация алгоритма на Python (lesson 6. filter kalman.py)

Давайте теперь посмотрим на результаты построения оценок рассмотренным алгоритмом. Реализуем на Python фильтр Калмана для решения описанной задачи: 

import numpy as np
import matplotlib.pyplot as plt
 
N = 100         # число наблюдений
dNoise = 1      # дисперсия шума
dSignal = 5     # дисперсия сигнала
r = 0.99        # коэффициент корреляции в модели движения
en = 0.1        # дисперсия СВ в модели движения
 
x = np.zeros(N)                         # истинные координаты перемещения (пока просто нули)
x[0] = np.random.normal(0, dSignal)     # формирование первой координаты
for i in range(1, N):                   # формирование последующих координат по модели АР
    x[i] = r*x[i-1] + np.random.normal(0, en)
 
z = x + np.random.normal(0, dNoise, N)  # формирование наблюдений
 
 
# фильтрация сигнала с помощью фильтра Калмана
xx = np.zeros(N)    # вектор для хранения оценок перемещений
P = np.zeros(N)     # вектор для хранения дисперсий ошибок оценивания
xx[0] = z[0]        # первая оценка
P[0] = dNoise     # дисперсия первой оценки
 
# рекуррентное вычисление оценок по фильтру Калмана
for i in range(1, N):
    Pe = r*r*P[i-1]+en*en
    P[i] = (Pe*dNoise)/(Pe+dNoise)
    xx[i] = r*xx[i-1]+P[i]/dNoise*(z[i]-r*xx[i-1])
 
# отображение результатов 
fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1, figsize=(10, 5))
 
ax1.plot(x)
ax1.plot(z)
ax1.plot(xx)
ax1.grid(True)
 
ax2.plot(P)
ax2.grid(True)
plt.show()

Видео по теме

#1: Метод наименьших квадратов

#2: Метод градиентного спуска

#3: Метод градиентного спуска для двух параметров

#4: Марковские процессы в дискретном времени

#5: Фильтр Калмана дискретного времени

#6: Фильтр Калмана для авторегрессионого уравнения

#7: Векторный фильтр Калмана

#8: Фильтр Винера

#9: Байесовское построение оценок, метод максимального правдоподобия

#10: Байесовский классификатор, отношение правдоподобия