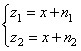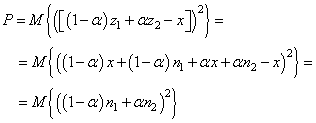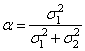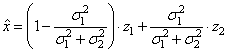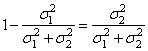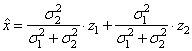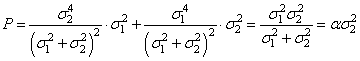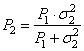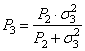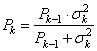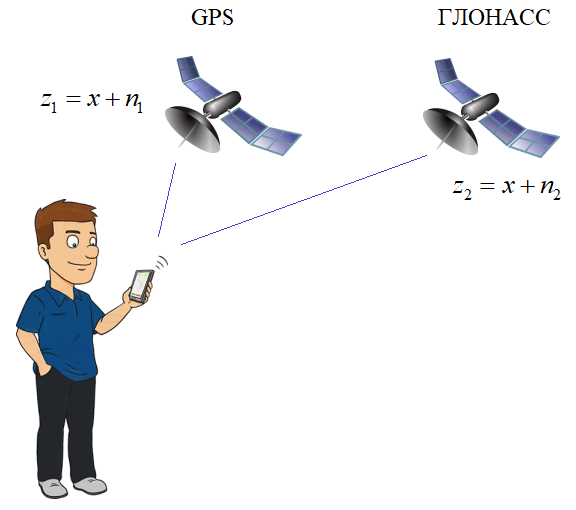
Фильтр Калмана дискретного времени

На этом занятии рассмотрим принцип работы одного, довольно популярного фильтра, который известен под названием «фильтр Кламана». Чтобы лучше понять этот материал, я решил рассмотреть его с позиций конкретного примера.

Предположим, что производятся наблюдения текущего местоположения координаты x стоящего на одном месте человека, используя два источника информации: ГЛОНАСС и GPS:

В определенный момент времени на входе устройства фиксируются наблюдения от этих систем навигации:

Причем, текущее значение полезного сигнала (координата x) искажаются аддитивными шумами:  - от GPS и  - от ГЛОНАСС. На практике часто такие шумы подчиняются нормальному закону распределения и имеют нулевое МО:

Здесь  - дисперсия (мера разброса значений от истинного значения x) для GPS, а  - для ГЛОНАСС. Причем, эти величины заранее известны из характеристик систем, и для простоты восприятия, можно положить:

Это примерные значения, используемые исключительно для этого занятия. Настоящие нужно смотреть по документации этих систем или из результатов предварительных экспериментов.

Итак, мы имеем два наблюдения  и задача прибора на основе этих величин вычислить значение полезного параметра x – координаты стоящего человека. Как бы мы ни старались, в общем случае найти точное значение x невозможно. Но можно вычислить приближенную величину (оценку), которую обозначим через . То есть, у нас должен быть некий математический алгоритм, который на выходе формирует эту оценку:

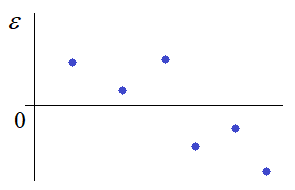
Здесь возникает две задачи: во-первых, как построить этот алгоритм и, во-вторых, как оценить качество работы этого алгоритма. Начнем со второй задачи, так как именно от критерия качества зависит вид алгоритма. Очевидно, что любой алгоритм будет приводить к ошибкам оценивания:

При наилучшем алгоритме эти ошибки от эксперимента к эксперименту будут, в среднем, колебаться вокруг нулевого значения, то есть, иметь нулевое МО:

И, понятно, что чем меньше ошибка, тем лучше. Но ее саму неудобно брать как критерий качества, т.к. может принимать и положительные и отрицательные значения, а нам бы хотелось сформировать критерий, который бы говорил: чем он больше, тем хуже работает алгоритм, чем меньше – тем лучше. Поэтому, в данном случае хорошо подходит квадрат ошибки и тогда критерий становится таким:

Но и здесь есть подводный камень: при одном эксперименте эта величина может быть небольшой, а при другом – намного больше. Поэтому логичнее было бы построить алгоритм, который бы минимизировал не конкретный квадрат ошибки, а в среднем давал бы как можно меньшие ошибки. Понятие в среднем – это, фактически, математическое ожидание, то есть, окончательно, наш критерий качества принимает вид:

Таким образом, нам нужно минимизировать дисперсию (разброс) ошибок оценивания.

Отлично, с этим разобрались. Как нам теперь построить алгоритм, который бы минимизировал этот критерий? Было доказано, что в случае гауссовских шумов минимум дисперсии ошибки обеспечивает следующий алгоритм:

где  - некие (пока неизвестные) весовые коэффициенты. И в данном случае от этих коэффициентов зависит величина критерия качества:

Однако, здесь задачу поиска двух коэффициентов можно свести к нахождению всего одного, если заметить, что:

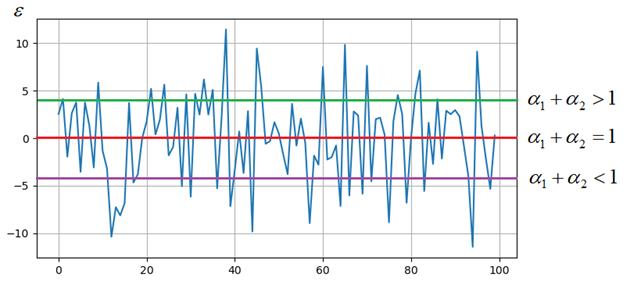
Почему это так? Когда мы с вами определяли величину ошибки:

то говорили, что хороший алгоритм делает ее среднее равное нулю. Так вот, если сумма коэффициентов будет больше 1, то, в среднем, будут получаться значения выше нулевого уровня. При сумме меньше 1 – ниже нулевого уровня и только при сумме равной 1 получим нулевое среднее ошибок, то есть, оценка на выходе алгоритма будет несмещенной.

В результате, наш алгоритм обработки наблюдений, принимает вид:

и критерий качества:

Распишем выражение под МО, учитывая, что

получим:

Учитывая независимость наблюдений и шумов, квадрат суммы распадается на сумму квадратов:

В итоге, мы выразили критерий качества непосредственно через дисперсии шумов наблюдений от каждого из источников. Этот критерий в зависимости от параметра α образует параболу с единственной точкой минимума. Из школьного курса математики мы знаем, что для нахождения точки минимума, нужно вычислить производную по параметру альфа и приравнять ее нулю:

откуда

Мы нашли оптимальное значение весового коэффициента, который будет минимизировать квадрат средних ошибок оценивания, а сам алгоритм обработки принимает вид:

или, учитывая, что

приходим к виду:

Что, фактически, означает эта формула? В действительности, мы здесь как бы взвешиваем два наблюдения и большее значение (вес) отдается тому, которое имеет меньшую дисперсию шума. Например, для значений

вес первого наблюдения будет выше второго. И это логично, т.к. первое наблюдение содержит, в среднем, более точную информацию о параметре x, чем второе. А вот если бы их дисперсии были одинаковыми, то оценка строилась бы как среднее арифметическое от наблюдений:

Полученный алгоритм оценивания можно воспринимать как частный случай реализации фильтра Калмана. И, в целом, отражает суть его работы: взвешивание двух наблюдений для формирования выходной оценки параметра.

Для оценки качества работы этого алгоритма, мы можем в формулу дисперсии ошибки оценивания:

подставить вычисленные значения для  и , получим:

Причем, отсюда видно, что оптимальное значение параметра α также равно отношению дисперсии ошибки оценивания на дисперсию шума второго наблюдения:

Сделаем последний шаг и приведем форму записи фильтра Калмана к рекуррентному виду. Смотрите, вот эту формулу:

можно представить и в таком виде:

или, подставляя вместо α выражение через дисперсию ошибок оценивания:

Именно в таком виде принято записывать фильтр Калмана в научной литературе. Эта формула, фактически, означает, что если наблюдения поступают на вход приемника последовательно друг за другом с определенным интервалом времени, то оценка по первому наблюдению, это просто:

с ошибкой оценивания

Когда приходит второе, с дисперсией шума , сначала пересчитывается дисперсия ошибки оценивания:

а, затем, уточняется оценка:

Получаем алгоритм рекуррентного построения оценок. Далее, когда придет еще одно наблюдение, допустим от GPS в следующий момент времени:

с дисперсией шума , мы можем уточнить ранее полученную оценку. Снова пересчитываем дисперсию ошибки оценивания:

и пересчитываем оценку:

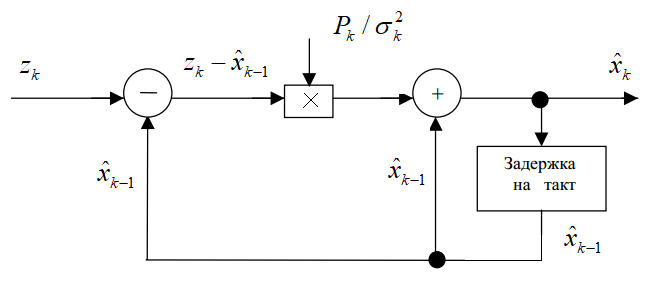
И так далее. Достоинством фильтра Калмана является возможность именно рекуррентного вычисления оптимальных оценок по наблюдениям, непрерывно поступающих на вход некоторого устройства. То есть, для любого k-го наблюдения, получим алгоритм пересчета:

и

Вот это выражение и представляет собой фильтр Калмана в дискретном времени.

То есть, по мере увеличения числа наблюдений мы будем получать все более точную оценку , доходя до определенного предельного уровня точности:

Причем, благодаря рекуррентному принципу работы фильтра, его вычислительная сложность остается постоянной при любом числе наблюдений – это его ключевая особенность.

Видео по теме

#1: Метод наименьших квадратов

#2: Метод градиентного спуска

#3: Метод градиентного спуска для двух параметров

#4: Марковские процессы в дискретном времени

#5: Фильтр Калмана дискретного времени

#6: Фильтр Калмана для авторегрессионого уравнения

#7: Векторный фильтр Калмана

#8: Фильтр Винера

#9: Байесовское построение оценок, метод максимального правдоподобия

#10: Байесовский классификатор, отношение правдоподобия