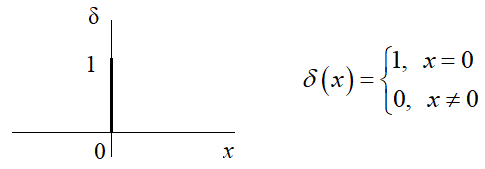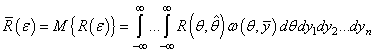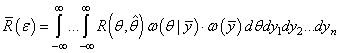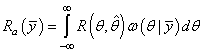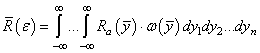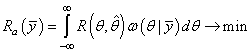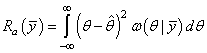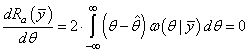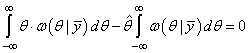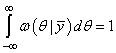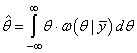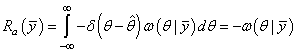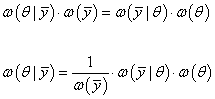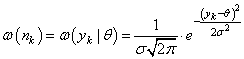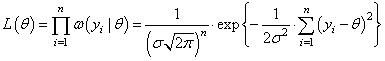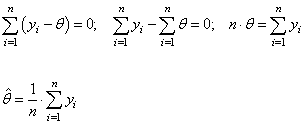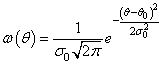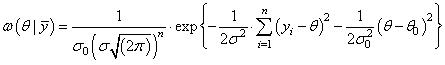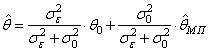|
Байесовское построение оценок, метод максимального правдоподобияНа этом занятии мы с вами рассмотрим общий принцип построения оценки неизменяемого, постоянного параметра. Пусть, этот параметр называется θ. Например, это может быть какая-либо координата стоящего на одном месте человека, или измерение дальности, до некоторого объекта или еще что-либо. Проблема в том, что мы не знаем точного значения этого параметра, а имеем лишь набор его наблюдений в отдельные моменты времени:
Например, каждое наблюдение может представлять этот параметр θ с добавкой некоторого шума наблюдения:
Наша задача
придумать алгоритм, который бы по наблюдениям
Здесь
И, также очевидно, что качество работы алгоритма должно быть связано с этой ошибкой. Но брать ее в чистом виде непрактично, т.к. она может быть и положительной и отрицательной, а нам бы хотелось иметь критерий, который бы принимал наименьшее значение для наилучшего алгоритма и увеличивался для более худших:
Поэтому при построении оптимальных байесовских оценок выбирают некоторую функцию, зависящую от ошибки:
так, чтобы ее минимум соответствовал лучшим оценкам, а увеличение означало более худшие оценки и, следовательно, более худшие алгоритмы оценивания. Такие функции получили название функции потерь. Например, это может быть квадратичная функция потерь:
или, простая функция потерь:
Здесь δ – это символ Кронекера:
Но сама по себе
эта функция является случайной величиной, так как при разных значениях
наблюдений
Учитывая, что:
получим:
И далее можно разделить наблюдения и параметр θ, выделяя функцию:
и
Из этих двух
последних формул хорошо видно, что для поиска наилучшей оценки параметра θ
достаточно минимизировать функцию
Чтобы конкретизировать эту формулу, необходимо выбрать конкретный вид функции потерь. Пусть это будет квадратическая функция:
Для нахождения ее минимума продифференцируем по θ и приравняем результат нулю:
Раскрываем скобки, интеграл распадается на два интеграла:
Так как площадь под функцией ПРВ равна 1, то
имеем:
Следовательно,
наилучшей оценкой параметра θ при квадратичной функции потерь
является математическое ожидание, вычисленное для апостериорного распределения
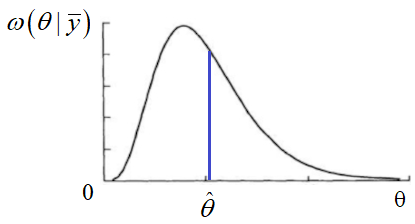
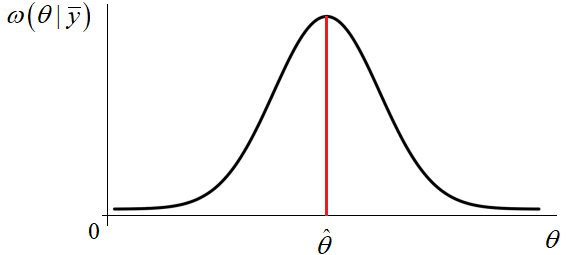
Если взять простую функцию потерь, получим:
И минимум достигается в точке максимума апостериорной ПРВ:
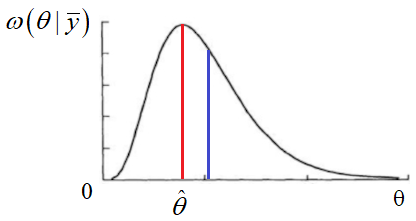
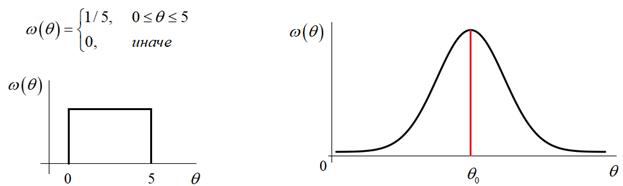
Из этого графика хорошо видно различие в построении оценки при простой и квадратической функциях потерь. То есть, при разных критериях качества, в общем случае будут получаться разные оценки. При этом, в вычислительном плане лучше подходит простая функция потерь, т.к. здесь достаточно определить лишь точку максимума условной ПРВ, тогда как при квадратической необходимо ее интегрировать и вычислять центр тяжести, что требует гораздо больше вычислений. Поэтому, на практике предпочитают использовать простую функцию потерь. Кроме того, для одного важного частного случая гауссовской ПРВ, оценки для этих функций потерь совпадают:
Поэтому здесь целесообразно выбирать именно простую функцию потерь, которая также минимизирует и квадратическую. Метод максимального правдоподобияНо, давайте подробнее рассмотрим, что значит найти точку максимума апостериорной ПРВ. Формально, ее можно расписать так:
Здесь первый
множитель представляет собой некоторое число, зависящее только от наблюдений Последний
множитель – это априорные сведения о параметре θ. Например, мы можем
знать, что он меняется в диапазоне от 0 до 5, тогда это можно представить в
виде равномерной ПРВ. Или же, мы знаем, что этот параметр находится где-то
вблизи некоторого значения
Однако, на практике часто эти сведения неизвестны и лучшее, что мы можем сделать в такой ситуации – это просто отбросить последний множитель и формула апостериорной ПРВ становится равной:
Здесь вторая
условная ПРВ
которая получила название функции правдоподобия. То есть, когда у нас нет априорных сведений о параметре θ и выбрана простая функция потерь, то лучшая оценка соответствует максимуму функции правдоподобия. И такая оценка получила название оценки максимального правдоподобия:
Чтобы конкретизировать эту формулу, положим аддитивную модель наблюдений:
с независимым гауссовским шумом:
В этом случае функция правдоподобия принимает вид:
Из этой формулы видно, что точка максимума будет достигаться, когда степень экспоненты минимальна:
Чтобы найти точку минимума достаточно продифференцировать это выражение по параметру θ и приравнять результат нулю:
Множитель перед суммой можно отбросить, получим:
То есть, при гауссовских независимых шумах достаточно усреднить имеющиеся наблюдения для вычисления оптимальной оценки по методу максимального правдоподобия. Конечно, если шум будет коррелирован или подчиняться другому закону распределения, то формула вычисления оценки также изменится. Это лишь частный пример построения такой оценки. Оценка по максимуму апостериорной ПРВЕсли у нас имеются дополнительные сведения об априорном распределении параметра θ, предположим, в виде гауссовской ПРВ:
то оценку, полученную по методу максимального правдоподобия можно уточнить и находить максимум уже апостериорной ПРВ:
В этом случае получим выражение вида:
Здесь также нужно найти минимум степени экспоненты:
Для этого дифференцируем это выражение по параметру θ и приравниваем результат нулю. Делая простые математические преобразования, получим алгоритм построения оценки:
где
то алгоритм
будет больше брать информацию из априорного значения, чем из оценки
то веса будут равны 0,5 и алгоритм вычислит среднее арифметическое этих двух величин:
И так далее. Вот так работает эта формула, которая позволяет уточнять оценку максимального правдоподобия дополнительной априорной информацией об оцениваемом параметре. Итак, на этом занятии мы с вами рассмотрели общий принцип построения байесовских оценок, получили выражение для простой и квадратической функций потерь, увидели как вычисляются оценки по методу максимального правдоподобия и возможность их уточнения при наличии дополнительной априорной информации. Видео по теме |