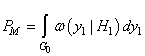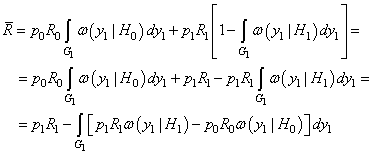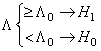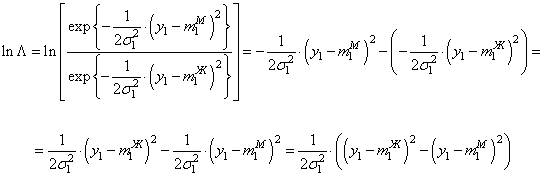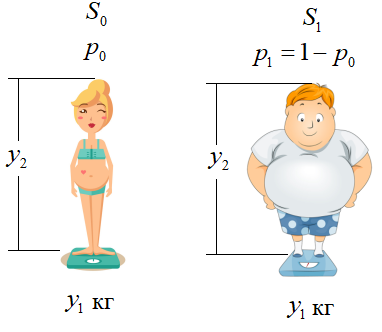
Байесовский классификатор, отношение правдоподобия

Смотреть материал на видео

Реализация алгоритма на Python (lesson 10. Recognize.py)

На этом занятии мы с вами рассмотрим известный и часто цитируемый в литературе алгоритм, различения сигналов на основе критерия Байеса. Предположим, что у нас имеются наблюдения роста и веса человека:

И по значениям этих наблюдений нужно сделать вывод: мужчина это или женщина. То есть, мы рассматриваем объект человек и этот объект может находиться в двух состояниях:

  •  - женщина;
  •  - мужчина.

с известными априорными вероятностями: . И, так как мужчин немного больше, чем женщин, то пусть эти вероятности равны:

Имея конкретные значения наблюдений , в общем случае, мы не можем точно сказать, кому они принадлежат, так как бывают мужчины с малым весом и ростом и результаты можно отнести к женщине и, наоборот, вес и рост отдельных женщин может напоминать мужские показатели. Поэтому можно лишь выдвинуть гипотезы:

  •  - женщина;
  •  - мужчина.

Соответственно, здесь возможны как верные результаты, так и ошибки. Это удобно представить в виде следующей таблицы:

True

True

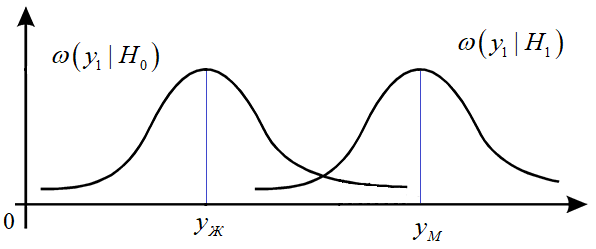
Здесь величина (вероятность) ошибки  - называется ошибкой 1-го рода и означает, что наблюдаемые значения были отнесены к мужчине, тогда как на самом деле являлись женскими. Вторая величина  называется ошибкой 2-го рода и означает, что мужские показания были трактованы как женские.

Например, если отдельно рассмотреть распределение веса мужчин и женщин, то их примерно можно представить следующими условными гауссовскими ПРВ:

Здесь  - среднестатистические показатели мужчин и женщин и относительно них имеется некоторый разброс значений: чем дальше отклонение от среднего веса, тем меньше встречается таких людей. Из этого рисунка хорошо видно, что при различении мужчин и женщин по весу, нам нужно установить некоторое пороговое значение L, например, вот так:

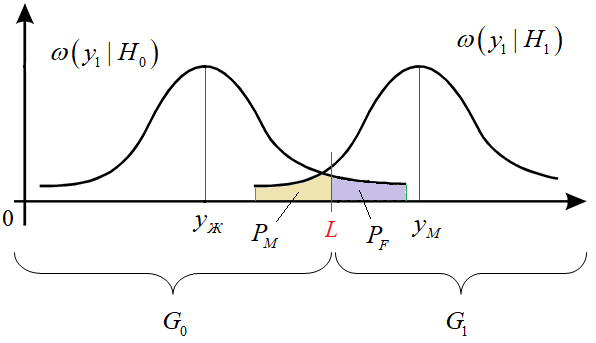
То есть, мы имеем две непересекающиеся области значений: . Если значение попадает в область , то делается предположение об истинности гипотезы :

иначе, выдвигается гипотеза :

Следовательно, вероятность 1-го рода, равна:

а вероятность 2-го рода:

Чтобы у нас интегрирования выполнялось в пределах одной области, например, , мы можем перейти к противоположной вероятности:

И далее, выбирать порог L так, чтобы минимизировать вероятности ошибок. Как вы понимаете, уменьшая одну, увеличиваем другую. Поэтому «разумный» критерий оптимального выбора должен быть построен на основе компромисса между вкладом двух типов возможных ошибок. Так вот, при байесовском подходе к задаче обнаружения каждой ошибке назначают определенный размер штрафа:

то есть, это числа и чем больше одно число по отношению ко второму, тем больший штраф назначается соответствующей ошибке. Например, если мы хотим меньше ошибаться при определении женщин по весу, то есть, иметь меньше ошибок , то следует взять штраф:

Если же нам в равной степени важны определение и мужчин и женщин, то штрафы следует выбирать равными:

Затем, используя эти величины, байесовский критерий качества формулируется как минимум средних ошибок:

Распишем формально этот критерий, получим:

Подставляя вместо  интеграл по области , имеем:

Та же картина будет наблюдаться, если мы обобщим этот результат на многомерный случай, то есть, будем использовать вектор наблюдений:

Очевидно, средние потери будут минимальны, если интеграл

будет максимален. Фактически, он определяет конфигурацию и правило выбора области . Смотрите, если текущее наблюдение  будет давать положительное значение выражения

то такой вектор следует отнести к области . А, как мы помним, в этой области принимается гипотеза . Значит, при выполнении этого неравенства должна выдвигаться гипотеза , а иначе – гипотеза .

Давайте перепишем это неравенство в более удобном виде:

Здесь справа записано число, а слева – отношение ПРВ. Данное неравенство получило название отношение правдоподобия и определяет оптимальное с точки зрения минимума средних байесовских потерь классификацию объектов. Часто его еще записывают в таких обозначениях:

и правило классификации принимает вид:

Давайте применим это правило к решению нашей задачи классификации мужчин и женщин на основе веса (чтобы не усложнять восприятие информации):

где  - нормальная СВ с нулевым средним и дисперсией . Далее, величину штрафов выберем одинаковой:

а априорные вероятности, как в начале нашего занятия:

Теперь у нас есть все для реализации алгоритма классификации. Только мы вместо изначального отношения правдоподобия возьмем натуральные логарифмы от величин:

Это упростит решение задачи и при этом не исказит работу алгоритма, т.к. неравенство при любой монотонной функции остается неизменным.

Итак, вычислим натуральный логарифм от отношения двух условных ПРВ, получим:

Выглядит громоздко, но в действительности, здесь простая школьная математика. Далее, все это сравнивается с порогом:

Реализация на Python

Реализуем это на Python, программа будет следующей: 

import numpy as np
 
def getL(y1, m1_F, m1_M, d1):
    res = 1/(2*d1)*((y1-m1_F)**2 - (y1-m1_M)**2)
    return res
 
def getL0(p0, p1):
    return np.log(p0/p1)
 
m1_F = 60   # средний вес женщин (кг)
m1_M = 85   # средний вес мужчин (кг)
 
d1 = 9     # дисперсия разброса веса (кг^2)
 
p0 = 0.48   # вероятность для женщин
p1 = 0.52   # вероятность для мужчин
 
N = 100     # число экспериментов
 
L0 = getL0(p0, p1)
 
nM = 0
for i in range(N):
    y1 = np.random.normal(m1_F, d1)
 
    L = getL(y1, m1_F, m1_M, d1)
 
    if(L >= L0):
        print("Мужчина", y1)
        nM += 1
    else:
        print("Женщина", y1)
 
error = nM/N*100
print(f"Ошибка: {np.round(error, 2)}%")

Видео по теме

#1: Метод наименьших квадратов

#2: Метод градиентного спуска

#3: Метод градиентного спуска для двух параметров

#4: Марковские процессы в дискретном времени

#5: Фильтр Калмана дискретного времени

#6: Фильтр Калмана для авторегрессионого уравнения

#7: Векторный фильтр Калмана

#8: Фильтр Винера

#9: Байесовское построение оценок, метод максимального правдоподобия

#10: Байесовский классификатор, отношение правдоподобия