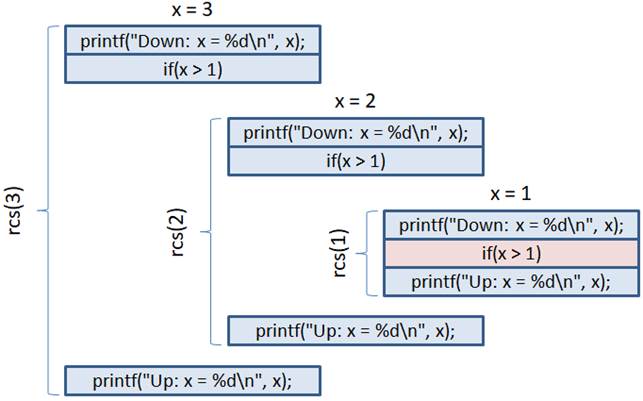
Рекурсивные функцииПрактический курс по C/C++: https://stepik.org/course/193691 На прошлом занятии мы увидели, что локальные переменные и значения аргументов функции при ее вызове помещаются в стековый фрейм. Благодаря такой организации данных у нас автоматически появляется довольно интересная возможность вызывать функции из самих себя с разными входными данными. Это называется рекурсией. А функции, которые это выполняют, рекурсивными. Давайте посмотрим на работу очень простой рекурсивной функции: Здесь функция rcs() пока значение параметра x больше единицы вызывает саму себя с аргументом x-1, то есть, на единицу меньше. Что в итоге будет происходить? При первом вызове в стек помещается значение параметра x=4 вместе с адресом возврата. Затем, отрабатывает первая функция printf() и на экране отображается строка: Down: x = 4 После проверки условия снова вызывается функция rcs(3) с аргументом 3. В стек помещается новое значение параметра x=3 и выполнение начинается с самого начала функции. Снова отрабатывает printf() с выводом на экран следующей строчки: Down: x = 3 И так далее. Для rcs(2) увидим строку: Down: x = 2 а для rcs(1) строчку: Down: x = 1 После этого переходим на проверку условия. Оно оказывается ложным, поэтому попадаем на вторую функцию printf(), которая выводит сообщение: Up: x = 1 Что происходит дальше? Из стека извлекается адрес возврата на вторую функцию printf(), указатель стека перемещается на предыдущий блок данных, в которых параметр x равен 2. Поэтому функция printf() отрабатывает с этим значением x=2. Видим на экране строку: Up: x = 2 На этом выполнение функции завершается. Снова берется из стека адрес возврата на вторую функцию printf(), указатель стека перемещается на блок с данными предыдущего вызова, в котором x = 3. Получаем строку: Up: x = 3 И также с последним вызовом: Up: x = 4 Условно рекурсивный вызов функции rcs() можно изобразить следующим образом:
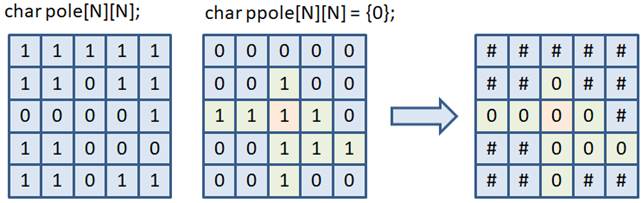
Сначала срабатывает rcs(3), затем, она вызывает функцию rcs(2), а та, в свою очередь, функцию rcs(1). Последняя функция не продолжает рекурсию, так как условие становится ложным. Сразу отрабатывает вторая функция printf() и текущий вызов завершает свою работу. Осуществляется переход (возврат) к вызывающей функции rcs(2). Она продолжает свое выполнение со второй функции printf(). Затем, также завершает свою работу и мы переходим к функции rcs(3). Вот принцип работы рекурсии. При этом, когда движение идет вглубь, то имеем прямой ход рекурсии, а при возврате – обратный ход. Максимальное число вызовов рекурсивной функции называют глубиной рекурсии. Пример использования рекурсивной функцииНадеюсь, общий принцип работы рекурсивных функций вам понятен. И, возможно, остается один важный вопрос, зачем они нужны и где имеет смысл их применять? Давайте для этого рассмотрим реальную практическую задачу. Предположим, у нас есть некоторое игровое поле pole размером 5х5 клеток и в каждой клетке может быть число от 0 до 255. Что это за числа и какую роль они несут сейчас совершенно неважно. Изначально все клетки поля закрыты от игрока. Эту информацию мы будем хранить во втором массиве ppole также размером 5х5. И будем полагать, если клетка ppole имеет значение 0, значит, она закрыта, а иначе открыта. Когда игрок открывает какую-либо клетку со значением 0 на игровом поле pole, то должны автоматически открываться все соседние клетки с нулевыми значениями, стоящие по горизонтали и вертикали. Открытые клетки мы будем помечать значением 1 в массиве ppole. Соответственно, при открытии центральной клетки должны получать следующую картину:
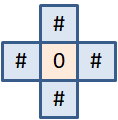
Эту задачу достаточно просто можно реализовать с помощью рекурсивной функции, например, так: #include <stdio.h> #define N 5 void show_pole(const char (*p)[N]) { for(int i = 0; i < N; ++i) { for(int j = 0; j < N; ++j) printf("%c ", (p[i][j] == 0) ? '#' : '0'); putchar('\n'); } } void open_zeros(const char (*p)[N], char (*pp)[N], int i, int j) { if(p[i][j] != 0 || pp[i][j] == 1) return; pp[i][j] = 1; // открываем клетку if(i-1 >= 0 && p[i-1][j] == 0) open_zeros(p, pp, i-1, j); if(i+1 < N && p[i+1][j] == 0) open_zeros(p, pp, i+1, j); if(j-1 >= 0 && p[i][j-1] == 0) open_zeros(p, pp, i, j-1); if(j+1 < N && p[i][j+1] == 0) open_zeros(p, pp, i, j+1); } int main(void) { char pole[N][N] = { {1, 1, 1, 1, 1}, {1, 1, 0, 1, 1}, {0, 0, 0, 0, 1}, {1, 1, 0, 0, 0}, {1, 1, 0, 1, 1}, }; char ppole[N][N] = {0}; show_pole(ppole); open_zeros(pole, ppole, 2, 2); puts("--------------------"); show_pole(ppole); return 0; } Здесь функция show_pole() отображает клетки игрового поля. А рекурсивная функция open_zeros() открывает все соседние клетки с нулевыми значениями. Работает она очень просто. Вначале мы передаем ей оба массива и индексы начальной открываемой клетки. Если текущая клетка игрового поля содержит 0, то она открывается и запускается рекурсия во все соседние клетки:
Если в соседних клетках также будет число 0, то она откроется, и рекурсия от нее продолжится дальше. И так, пока вся группа связанных нулевых клеток не будет открыта. После запуска программы увидим следующий результат: #
# # # #
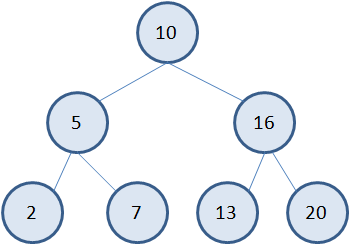
Как видите, все нужные клетки были открыты. Вообще рекурсивные функции очень удобны, когда нам нужно перебрать некие иерархические данные, которые имеют сложную структуру, и обычными циклами их проходить было бы затруднительно. В частности, рекурсия используется для переборов вершин бинарных деревьев – довольно распространенной структуры данных следующего вида:
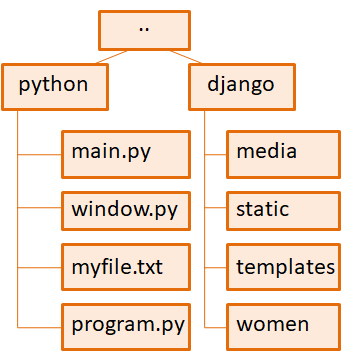
Или для перебора каталогов и файлов:
И так далее. Везде, где присутствует иерархичность можно подумать об использовании рекурсивных функций. Но нужно всегда помнить и об их недостатках. Они следующие:
Практический курс по C/C++: https://stepik.org/course/193691 Видео по теме |